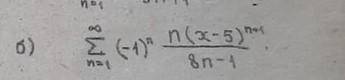
Пошаговое объяснение:
1)
а. 8а + 19а - 28а + 3а = 2а
б. 2,3а +1,8 - 3,2а - 2,4 = -0,9а - 0,6
в. -4х - 11х + 35х - 38х = - 18х
г. 1,6с - 1,2 -3,1с + 0,8 = -1,5с - 0,4
д. 1,1а + 0,9с - 1,2 - 1,3а - 3,8с = -0,2а - 2,9с - 1,2
2)
а. 2 (7а - 6) - 9а = 14а - 12 - 9а = 5а - 12
б. -5х - 4 (8 - 3х) = -5х - 32 - 12х = -17х - 32
в. -3 (2m - 5) - 8 (1 - 6m) = -6m - 15 - 8 - 48m = -54m - 23
г. -7 (3а - 2b) + 2 (5а + 2b) = -21а - 14b + 10а + 4b = -11а - 10b
3)
д. am + bm = m (a + b)
е. 3х - 6у + 9z = общего множителя нет
ж. 5m + 5n - 5 = 5 (m + n)
До чего ленивая молодежь пошла, им уже даже пишут, какие правила использовать, а они... Не учатся ничему и учиться не хотят... :)
Пошаговое объяснение:
1) Производная произведения: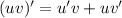
Правило дифференцирования сложной функции: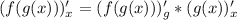
(индекс внизу означает, по какой переменной дифференцируем, * означает умножение)
тогда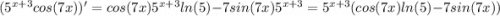
2) Дифференцирование сложной функции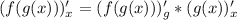
Примем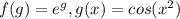
Дифференцируем f(g):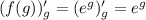
Дифференцируем g(x):
Тогда
3) Как и в 2, дифференцируем сложную функцию
4) Производная суммы есть сумма производных:
Окончательно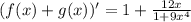
5) Опять производная сложной функции: