Для всех равных пар натуральных чисел
Пошаговое объяснение:
Пусть канонические виды чисел x и y таковы:
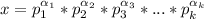
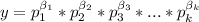
где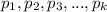 
- простые числа, а
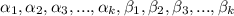- целые неотрицательные степени простых чисел (некоторые могут равняться нулю).
Тогда по свойству НОД(x; y)=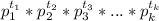
где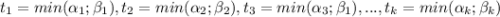 
По условию НОД(x; y)²=x · y и отсюда следует, что
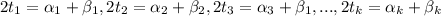
Очевидно, что значение min(m; n) или m или n. Поэтому, если
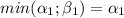, то из равенства 
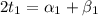следует, что 
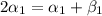и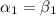 
. Точно такое равенство можно установить если 
.
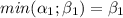И такие равенства получаются для других степеней простых чисел.
Отсюда заключаем, что НОД(x; y)²=x · y, тогда и только тогда, когда x=y.
Отсюда следует ответ к задаче: для всех равных пар натуральных чисел.
2068+1034=3102