x1=1/3; x2=3
Пошаговое объяснение:
x+1/x=3целых 1/3
мы превращаем 3ц 1/3 в неправильную дробь:
х+1/х=10/3.
преобразуем уравнение, перенося 10/3 в другую сторону(меняется знак) и приравниваю к 0:
х+1/х-10/3=0
Наименьший общий знаменатель 3, значит приводим к общему знам уравнение
3х²+3-10х/3х=0
По ОДЗ избавляемся от знам. ОДЗ х не равно 0
Получаем квадратное уравнение. Ставим все компоненты на свои места.
3х²-10х+3=0
раскладываем на множители, плоучаем
(3х-1)×(х-3)=0
3х-1=0
х-3=0
решаем ур-е относителтно х и получаем два корня
х=1/3 и х=3
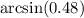
Будем вычислять значение данного выражения с формулы:
![f(x_{0} + ∆x) \approx f(x_{0}) + d[f(x_{0})]](/tpl/images/1445/8893/6692e.png)
Составим функцию f(x):
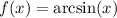
По условию нам нужно вычислить значение данной функции в точке 0.48.
Смотрим на левую часть формулы:
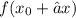
В качестве х₀ выбираем число, arcsin которого мы можем вычислить и которое находится близко к числу 0.48. Таким числом является 0.5, ведь оно ближе всего к 0.5, и его arcsin:
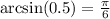
Поэтому х₀ = 0.5. Следовательно ∆х = 0.48 - 0.5 = -0.02.
Что мы получили:
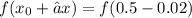
Далее работаем с правой частью формулы:
![f(x_{0}) + d[f(x_{0})]](/tpl/images/1445/8893/6d709.png)
Сначала вычислим значение функции в точке х₀. Собственно мы это сделали ранее:
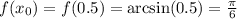
Дифференциал в точке х₀ найдём по формуле:
![d[f(x_{0})] = f'(x_{0})∆x](/tpl/images/1445/8893/3d87a.png)
Берём производную от нашей функции:
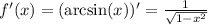
Находим её значение в точке х₀:
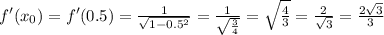
Таким образом:
![d[f(x_{0})] = \frac{2 \sqrt{3} }{3} \times ( - 0.02) = - \frac{4 \sqrt{3} }{3 \times 100} = - \frac{ \sqrt{3} }{75}](/tpl/images/1445/8893/456f4.png)
Итого:
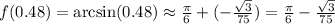
Вычислим окончательное приближенное значение:
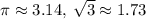
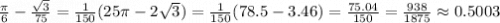
ответ: arcsin(0.48) ≈ 0.5003
72/90,12/90, 10/90,5/90