ясно, что двигаясь вниз и вправо, независимо от формы пути, фоксу нужно будет сделать 6 ходов, чтобы из левой верхней клетки попасть в правую нижнюю. из этих шести ходов 3 обязательно будут на одну клетку вниз, а 3 - на одну клетку вправо. поскольку после каждого ходачисло под фишкой меняется, то имеем перестановку из 6 элементов двух разных типов, по три каждого типа. чтобы подсчитать общее количество вариантов достижения правой нижней клетки применяем формулу для числа перестановок n элементов с повторениями:
p = n! / (n1! где n=6; n1=3 и n2=3.
подставляя, получаем
p=6! / (3! 3! )=720/36=20
ответ: 20
S=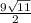
; V=3
Пошаговое объяснение:
Даны координаты пирамиды: A1(1,3,1), B(-1,4,6), C(-2,-3,4), D(3,4,-4)
Объем пирамиды, построенной на векторах AB(X1;Y1;Z1), AC(X2;Y2;Z2), AD(X3;Y3;Z3) равен:
![V=\frac{1}{6} *\left[\begin{array}{ccc}X1&Y1&Z1\\X2&Y2&Z2\\X3&Y3&Z3\end{array}\right]](/tpl/images/1006/5318/91605.png)
здесь X,Y,Z координаты вектора.
Найдем вектора:
AB(-2;1;5)
AC(-3;-6;3)
AD(2;1;-5)
![V=\frac{1}{6} *\left[\begin{array}{ccc}-2&1&5\\-3&-6&3\\2&1&-5\end{array}\right]](/tpl/images/1006/5318/e8aa7.png)
= 
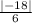= 3
Где (-18) нашли как определитель матрицы.
∆ = -2*((-6)*(-5) - 1*3) - -3*(1*(-5) - 1*5) + 2*(1*3 - (-6)*5) = -18
Площадь грани ACD находим как половину модуля векторного произведения векторов AC и AD
AC(-3;-6;3)
AD(2;1;-5)
S=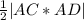
векторное произведение
AC*AD = = i ((-6)·(-5) - 3·1) - j ((-3)·(-5) - 3·2) + k ((-3)·1 - (-6)·2) = i (30 - 3) - j (15 - 6) + k (-3 + 12) = {27; -9; 9}
Модуль вектора
|AC*AD| =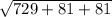 
= √891 = 9√11
S=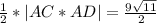 
0,00000000000000000000000000000000000001
0,000001