a + b + c = 72
a : b = 3 : 5
b : c = 7 : 8
Домножим первую пропорцию на 1,4 (чтобы уравнять b)
a : b = (3·1,4) : (5·1,4) = 4,2 : 7
Получаем новую пропорцию
a : b : c = 4,2 : 7 : 8
Пусть k - коэффициент пропорциональности, тогда а = 4,2k; b = 7k; c = 8k. Уравнение:
4,2k + 7k + 8k = 72
19,2k = 72
k = 72 : 19,2
k = 3,75
a = 4,2 · 3,75 = 15,75
b = 7 · 3,75 = 26,25
c = 8 · 3,75 = 30
ответ: 15,75; 26,25 и 30.
Проверка:
а : b = 3 : 5 = 15,75 : 26,25 = 0,6 - отношение первого числа ко второму
b : c = 7 : 8 = 26,25 : 30 = 0,875 - отношение второго числа к третьему
a + b + c = 15,75 + 26,25 + 30 = 72 - сумма трёх чисел
Пошаговое объяснение:
Задача на комбинаторику.
В комбинаторике разделяют два типа задач: на сочетания и размещения.
Сочетание - это тип задач в комбинаторике, в которых порядок элементов не важен.
Размещение - это тип задач в комбинаторике, в которых порядок элементов важен.
У нас задача на размещение.
Формула для решения задач на размещения:
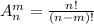
Где n - общее количество карт в колоде; m - количество вальтов; дам.
Подставляем значения в формулу:
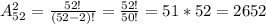
Напоминаю, что 52! это - 1 * 2 * 3 * 4 * 5 * 6 ... * 52.
Следовательно, 50! это - 1 * 2 * 3 * 4 * 5 * 6 ... * 50
52! и 50! можем сократить на 50!, в числителе останется 51 * 52, а в знаменателе - 1(мы числитель и знаменатель всегда можем домножить на единицу).
Получаем
Решаем пункт б:
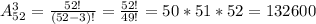
Все то же самое, что и в пункте а.
Задача решена.
53х-46х=3139-465
7х=2674
х=2674:7
х=382