ответ: r = 3√15/4
S = 63√15 / 8
Объяснение:
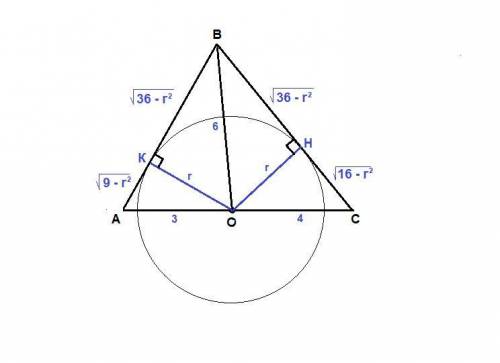
ОК⊥АВ и ОН⊥ВС как радиусы, проведенные в точки касания.
ОК = ОН = r,
ОВ - общая сторона для треугольников ВОК и ВОН, ⇒
ΔВОК = ΔВОН по катету и гипотенузе, ⇒
∠ОВК = ∠ОВН, ⇒
ВО - биссектриса угла АВС.
Из прямоугольных треугольников по теореме Пифагора выразим отрезки сторон АВ и ВС:
AK = √(9 - r²)
KB = √(36 - r²)
BH = √(36 - r²)
HC = √(16 - r²), тогда
АВ = √(9 - r²) + √(36 - r²)
ВС = √(16 - r²) + √(36 - r²)
По свойству биссектрисы угла треугольника:
АВ : ВС = АО : ОС
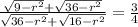
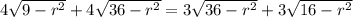

Возводим обе части уравнения в квадрат:
16(9 - r²) + 8√(36 - r²)√(9 - r²) + 36 - r² = 9(16 - r²)
144 - 16r² + 8√(36 - r²)√(9 - r²) + 36 - r² = 144 - 9r²
8√(36 - r²)√(9 - r²) = 8r² - 36
2√(36 - r²)√(9 - r²) = 2r² - 9
Возводим в квадрат еще раз:
4(36 - r²) · (9 - r²) = 4r⁴ - 36r² + 81
4(324 - 45r² + r⁴) = 4r⁴ - 36r² + 81
1296 - 180r² + 4r⁴ = 4r⁴ - 36r² + 81
144r² = 1215
r² = 135/16
r = 3√15/4
AB = √(9 - 135/16) + √(36 - 135/16) = √((144 - 135) / 16) + √((576 - 135) / 16) =
= √(9/16) + √(441/16) = 3/4 + 21/4 = 24/4 = 6
BC = √(36 - 135/16) + √(16 - 135/16) = 21/4 + √((256 - 135) / 16) =
=21/4 + √(121/16) = 21/4 + 11/4 = 32/4 = 8
Полупериметр:
p = (AB + BC + AC)/2 = (6 + 8 + 7)/2 = 21/2
S = pr
S = 21/2 · 3√15/4 = 63√15/8
Для единицы поверхности звезды, в соответствии с законом Стефана –Больцмана можно записать соотношение: Е = а*Т^4. Здесь Е – энергетическая светимость единицы поверхности звезды; а – постоянная Стефана-Больцмана; Т - абсолютная температура поверхности звезды. Используя эту формулу можно найти соотношение энергетических светимостей единиц поверхности звезды и Солнца. Ес/Ез = а*Тс^4/а*Тз^4 = Тс^4/Тз^4 = (Тс/Тз)^4 = (6000/4000)^4 =1,5^4 = 5,0625. Таким образом, светимость единицы поверхности Солнца из-за большей температуры больше в 5 с лишним раз, нежели светимость единицы поверхности заданной звезды. Но суммарная светимость заданной звезды в 400 раз больше суммарной светимости Солнца. Так произошло потому, что площадь поверхности заданной звезды больше площади поверхности Солнца. Больше во столько раз, во сколько раз могла бы быть больше суммарная светимость звезды, если бы она имела температуру Солнца. Таким образом, площадь поверхности заданной звезды в 5,0625*400 = 2025 раз больше площади поверхности Солнца. С некоторым приближением, будем считать, что звезда и Солнце имеют форму шара. Площадь поверхности шара определяется выражением S = π*d^2. Здесь d - диаметр шара. Отношение площадей нами найдено, тогда можно записать Sз/Sс =π*dз²/π*dс² = dз²/dс² = (dз/dс)²= 2025. Отсюда dз/dс = √2025 = 45. Заданная звезда больше Солнца в 45 раз.
115+295=410 (болельщиков) - в Соснограде
410-300=110 (болельщтков) - в Кошкино
940-(115+410+110)=9 40-635=305 (болельщиков) - в Голубых елях
940:5=188 (тентов) - нужно заготовить оганизаторам