5 и 12
Пошаговое объяснение:
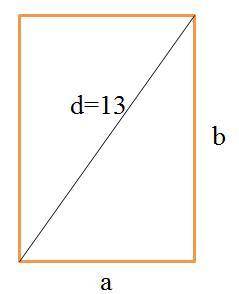
Пусть стороны прямоугольника a и b, диагональ d. Площадь прямоугольника равна: S = a · b. По условию a · b = 60, а диагональ d = 13.
Диагональ делит прямоугольник на два прямоугольных треугольника и поэтому верна теорема Пифагора: d² = a² + b².
На основе условий задачи получаем систему уравнений:
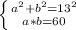
Второе уравнение умножим на 2 и прибавим к первому:
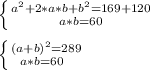
a и b стороны прямоугольника и поэтому a+b>0:
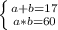
Решаем систему методом подстановки:
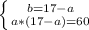
a²-17·a+60=0
D=(-17)²-4·1·60=259-240=49=7²
a₁=(17-7)/2=10/2=5, тогда b₁ =17-5=12
a₂=(17+7)/2=24/2=12, тогда b₂ =17-12=5.
Отсюда, ответом будут 5 и 12.
Из того,что я вижу,это карманный вычислитель степеней до куба и корней(квадратных и кубических).Посередине должно стоять число,над которым ты хочешь провести операции,на данный момент у тебя число пи(3.14),сверху его квадрат и куб,а снизу квадратный и кубический корень.
Пошаговое объяснение:
Мотаешь катушку справа и числа меняются(какие там есть,увы,знать не могу)
n - означает неизвестно число,а справа от отверстий операции,которые с ним проводят
Называется либо математическим кругом,либо шпаргалкой
Доказать, что из 27 учеников класса, знающих 163 стихотворения, найдется хотя бы один, который знает не менее 7 стихотворений.
Принцип Дирихле. При любом распределении kn + 1 или больше предметов по n ящикам в одном ящике окажется не меньше, чем k + 1 предмет (n∈Z).Допустим, что каждый из 27 ребят знает не больше 6 стихотворений.
Тогда вместе они знают не более 162 стихотворений:
27 · 6 = 162
А по условию общее количество стихотворений составляет 163.
Следовательно, наше предположение не верно, и хотя бы один из ученик знает больше 6 стихотворений, а значит не менее 7.
Доказано.
Обозначим длину прямоугольника как а, ширину прямоугольника как b, и диагональ как c.
Рассмотрим ΔABC: ∠B=90° ⇒ ΔABC - прямоугольный; a,b - катеты, c - гипотенуза
т. Пифагора гласит:
a² + b² = c²
a² + b² = 13²
a² + b² = 169
А площадь прямоугольника находится по формуле:
S = a * b
a * b = 60
Составим систему уравнений и решим методом подстановки.
Вводим новую переменную.
b² = t - новая переменная.
b² = t
b² = 25 или b² = 144
b₁ = 5; b₂=-5; b₃=12; b₄=-12
Т.к. сторона не может быть отрицательна, то -5 и -12 не подходят.
a * b = 60
a₁ * 5 = 60
a₁ = 12
a₂ * 12 = 60
a₂ = 5
⇒ Стороны прямоугольника равны 5 см и 12 см.
ответ: 5 см; 12 см