Составить уравнение нормали и касательной к кривой y = x -x³ в точке с абсциссой x₀ = -1.
Уравнение касательной к кривой y = x -x³ в точке с абсциссой x₀ = -1
имеет вид y - y₀ =k₀(x- x₀),где k₀ угловой коэффициент касательной к кривой в точке x₀ .
При x = x₀ = -1 ⇒y₀ = (-1) -(-1)³ =0 . Значит y - 0 =k₀(x- -(-1)) ⇔
y =k₀(x+1).
Определяем угловой коэффициент касательной в точке x₀
y ' =(x-xx³) ' = x ' - (x³) ' =1 -3x² .
k₀ = y '(x₀) = y '(-1) = (1 -3*(-1)²) = -2 .
Окончательно уравнение касательной к кривой в точке x₀ будет :
y = -2(x+1) ⇔ y = -2(x+1) .
Уравнение нормали к кривой в точке x₀ имеет вид y - y₀ =k₁(x- x₀) ,где угловой коэффициент нормали к₁ = -1/к₀=1/2 , поэтому уравнение нормали будет y =1/2(x-1) ⇔y =0,5x - 0,5.
 и
и 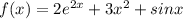 , x∈R
, x∈R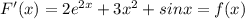
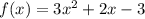 и
и 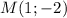
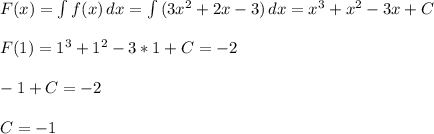
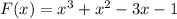
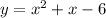 и прямая y = 0 (ось Ох).
и прямая y = 0 (ось Ох). 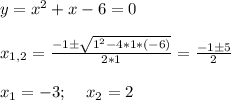
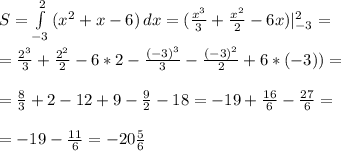
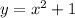 и прямая
и прямая 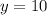 .
.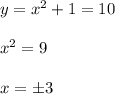
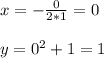
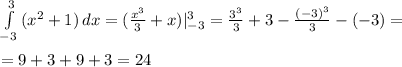
3мин.42с = (3 х 60)с + 42с = 222с
8час.27мин = (8 х 60) мин + 27 мин = 507мин.
83 т = 830ц (т.к. в 1т =10ц)
Вычисление по действиям:
14т 30 кг - 5т407кг - 688000г , все значения превращаем в г
14030000г - 5407000г - 688000г = 7935000г
1) 14030000 - 5407000 = 8623000
2) 8623000 - 688000 =7935000
7935000г = 7935кг. = 7т 935кг