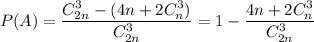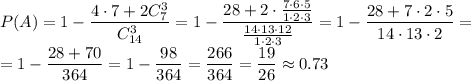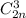
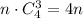logo
Вход Регистрация Спроси Mozg AI
М
Молодежь
К
Компьютеры-и-электроника
Д
Дом-и-сад
С
Стиль-и-уход-за-собой
П
Праздники-и-традиции
Т
Транспорт
П
Путешествия
С
Семейная-жизнь
Ф
Философия-и-религия
Б
Без категории
М
Мир-работы
Х
Хобби-и-рукоделие
И
Искусство-и-развлечения
В
Взаимоотношения
З
Здоровье
К
Кулинария-и-гостеприимство
Ф
Финансы-и-бизнес
П
Питомцы-и-животные
О
Образование
О
Образование-и-коммуникации
нурик200120
нурик200120
30.01.2023 14:24 •  Математика

Определённые интегралы210 а211 а212 а213 а214 а

👇
Увидеть ответ
Ответ:
pollyshtal33333333
pollyshtal33333333
30.01.2023
  все просто. решая совместно, получим
4,7(42 оценок)
Открыть все ответы
Ответ:
tisha199567
tisha199567
30.01.2023
Знак корня №
высота правильного треугольника h=№3*а/2, где а сторона треугольника
а=h*2/№3=10/№3
высота пирамиды есть отрезок, соединяющий центр вписанной окружности (центроид) и вершину. центр окружности - это точка пересечения, высот, медиан и биссектрис. r=a*№3/6=(10/№3)*№3/6=10/6=5/3
Треугольник, образованный радиусом, высотой и апофемой - прямоугольный. Зная катет (радиус) и угол (двугранный) между ним и гипотенузой (апофемой),второй катет (высота пирамиды)=r*tq 45=r=5/3
апофема=5*№2/3
Площадь основания=а*н/2=(10/№3)*5/2=25/№3
Боковая поверхность=3*а*апофему=3*10*5*№2/3*№3=50*№2/№3
Общая площадь равна сумме боковой и основания=(25+50*№2)/№3
4,8(61 оценок)
Ответ:
микадо1
микадо1
30.01.2023
Решим задачу в общем случае. Обозначим число сторон в основании призмы за n. Тогда призма имеет n граней и 2n вершин.
Вероятность рассчитывается как отношение числа благоприятных исходов к общему числу исходов.
Найдем общее число исходов: выбрать 3 вершины из 2n имеющихся можно C_{2n}^3
Найдем число благоприятных исходов как разность общего числа исходов и числа неблагоприятных исходов. Общее число исходов известно, теперь находим число неблагоприятных исходов.
Если все выбранные вершины лежат на боковой грани или на основании, то образовавшееся сечение не будет содержать точек строго внутри призмы. Число выбрать три вершины боковой грани равно n\cdot C_4^3=4n, так как призма имеет n боковых граней, и в каждой грани расположено 4 вершины. Число выбрать три вершины основания равно 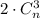2\cdot C_n^3, так как призма имеет всего два основания и в каждом из этих оснований расположено n вершин.
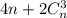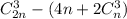Получаем общее число неблагоприятных исходов: 4n+2C_n^3. Тогда число благоприятных исходов равно C_{2n}^3-(4n+2C_n^3).
Находим искомую вероятность:
P(A)= \dfrac{C_{2n}^3-(4n+2C_n^3)}{C_{2n}^3} =1- \dfrac{4n+2C_n^3}{C_{2n}^3}
Для семиугольной призмы, то есть для n=7, получаем:
P(A)= 1- \dfrac{4\cdot7+2C_7^3}{C_{14}^3} =1- \dfrac{28+2\cdot \frac{7\cdot6\cdot5}{1\cdot2\cdot3} }{ \frac{14\cdot13\cdot12}{1\cdot2\cdot3} } =
1- \dfrac{28+7\cdot2\cdot5 }{14\cdot13\cdot2 } =
\\\
=1- \dfrac{28+70 }{364 } =1- \dfrac{98 }{364 } =\dfrac{266}{364 }=\dfrac{19}{26} \approx0.73
ответ: 0.73
4,8(76 оценок)
Это интересно:
К
Как использовать галогенную печь: простой и быстрый гид...
О
Секреты общения с глухими людьми: как научиться понимать и быть понятым...
С
Остановите драку! Как сделать так, чтобы ваш малыш перестал драться...
К
Изучаем, как создать общедоступный календарь в Outlook...
К
Как получить очки отряда в Call of Duty Ghosts?...
О
Как создать комиксы в стиле Манга...
О
Как поступить в Техасский аграрный университет...
О
Как использовать логарифмические таблицы: практическое руководство...
К
Как экспортировать историю чата Skype на компьютерах Windows и Mac...
З
Здоровье
02.09.2020
Польза и способы приема пчелиной пыльцы...
Новые ответы от MOGZ: Математика
Gen04
Gen04
20.01.2023
Проведи в прямокутнику дві лінії так щоб утворилося 8 трикутників...
Маслинка174
Маслинка174
20.01.2023
Из nпион сделали букеты по 3белых и r красных пиона в каждом. сколько вышло букетов...
ElementalOfChaos
ElementalOfChaos
20.01.2023
Одно из чисел суммы-9 букв заранее большое...
Alenasol1
Alenasol1
20.01.2023
Увалеры есть попугайчики и хомячки у всех 5 голов и 16 ног сколько у валеры попугайчиков и сколько хомячков....
arina121212
arina121212
20.01.2023
Білочка у першій схованці знайшла 5 горішків,а у другій у 3 рази більше.скільки всього горішків знайшла білочка?...
vvkim87
vvkim87
20.01.2023
Решить выражение 300 -(90+70)+(86-46) подскажите порядок действий...
kristiniiiiiii
kristiniiiiiii
20.01.2023
Как состарить бумагу в условиях? чтобы потом можно было писать. и да, старение бумаги уже с написанным текстом происходит также? заранее...
d7175944p0ajvy
d7175944p0ajvy
20.01.2023
Петрик вирізав сніжинок у три рази менше, ніж вони із сестрою вирізали разом. у скільки разів петрик вирізав сніжинок менше, ніж сестра?...
luizaorlova99
luizaorlova99
20.01.2023
Найдите по формуле s=ut путь, если : а)u=3км/ч,t=6ч;...
maryanazarfdFj
maryanazarfdFj
20.01.2023
Мальчик купил 3альбома по 1грн 65к за каждый.сколько денег дал кассиру мальчик,если получил сдачу 1грн 18к.?...

MOGZ ответил

Полный доступ к MOGZ
Живи умнее Безлимитный доступ к MOGZ Оформи подписку
О НАС
ПОМОЩЬ
App
.
.
logo
Вход Регистрация
Что ты хочешь узнать?
Спроси Mozg
Открыть лучший ответ