Область определения выражения - это множество значений, при которых данное выражение имеет смысл. Другими словами, это те значения х, которые можно подставить в данное выражение.
Искать область определения лучше всего методом исключения - отбрасывая все значения, при которых выражение теряет математический смысл.
1) Если в выражении есть знаменатель с переменной, то знаменатель не равен 0.
Пример:
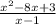
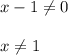
Область определения:
x∈(-∞; 1)∪(1;+∞)
2) Логарифмическое выражение. Основание логарифма определено при a>0 за исключением a=1. Выражение под знаком логарифма должно быть больше нуля.
Пример:
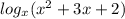
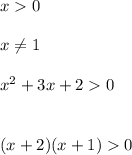
x∈(0; 1)∪(1; +∞)
3) Иррациональные выражения четной степени. Подкоренное выражение должно быть ≥0.
Пример:
![\sqrt[4]{x+10}](/tpl/images/0605/4384/6e133.png)
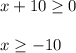
x∈[-10; +∞)
Также бывают более сложные и комбинированные выражения. При нахождении области определения всего выражения необходимо учесть все моменты, которые могут привести к ограничению этой области.
Пример:
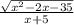
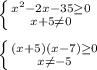
x∈(-∞; 5)∪[7; +∞)
Нам нужно доказать, что это число делится на 6 <=> делится на 2 и на 3.
Докажем, что число ab(a - b)(a + b) делится на 2. Если хотя бы одно из чисел а и b четно, то все нормально. Если a и b нечетные, то разность (a - b) делится на 2 и тоже вче нормально.
Докажем, что число ab(a - b)(a + b) делится на 3. Если хотя бы одно из чисел a и b делится на 3, то все нормально. Если числа a и b не делятся на 3, но дают одинаковые остатки при делении на 3, то разность (a - b) делится на 3. Если числа a и b не делятся на 3 и дают разные остатки при делении на 3, то сумма (а + b) делится на 3.
Значит, число ab(a² - b²) = ab(a - b)(a + b) делится на 2 и на 3, значит и на 6.