Докажем, что пяти достаточно.
Пусть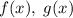 
два многочлена четвертой степени, которые совпадают в пяти точках. Тогда 
является многочленом, имеющим пять корней. Но степень многочлена
Четырех может быть недостаточно: Всего у многочлена четвертой степени пять коэффициентов, значит, пять неизвестных. Четыре уравнения не всегда дают единственное решение.
Можно доказать и более общий результат:
Если 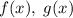— многочлены, степени 
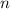, то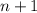 
— минимальное количество точек, в которых достаточно проверить совпадение многочленов, чтобы доказать их тождественное равенство.
База: для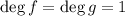 
все очевидно: по аксиоме требуется две точки для однозначного определения прямой.
Переход: пусть для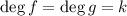 
верно. Докажем истинность для 
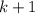. Для этого предположим обратное: достаточно 
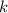точек. Возьмем различные многочлены 
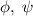степени
б) 16/40=2/5=18/45 28/36=7/9=63/81
в) 48/72=2/3=200/300 35/105=1/3=2/6