Sabcd = 25 ед².
Пошаговое объяснение:
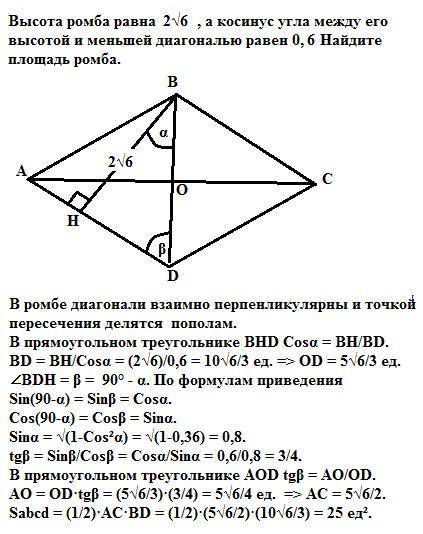
В ромбе диагонали взаимно перпенликулярны и точкой пересечения делятся пополам.
В прямоугольном треугольнике ВНD Cosα = BH/BD.
BD = BH/Cosα = (2√6)/0,6 = 10√6/3 ед. => ОD = 5√6/3 ед.
∠BDH = β = 90° - α. По формулам приведения
Sin(90-α) = Sinβ = Cosα.
Cos(90-α) = Cosβ = Sinα.
Sinα = √(1-Cos²α) = √(1-0,36) = 0,8.
tgβ = Sinβ/Cosβ = Cosα/Sinα = 0,6/0,8 = 3/4.
В прямоугольном треугольнике AOD tgβ = AO/OD.
AO = OD·tgβ = (5√6/3)·(3/4) = 5√6/4 ед. => AC = 5√6/2.
Sabcd = (1/2)·AC·BD = (1/2)·(5√6/2)·(10√6/3) = 25 ед².
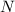деталей, с первого за это же время успевает выйти в два раза больше деталей, т.е. 
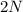. А всего с двух конвейеров выходит 
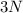деталей. Тогда удобно рассмотреть период времени, когда выпускается некоторое большое число деталей, кратное трём. Возьмём для дальнейших рассуждений такой период, за который выпускается 
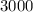деталей.
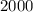деталей и из них 
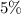, т.е. 
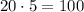бракованных.
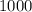деталей и из них 
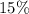, т.е. 
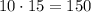бракованных. 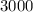деталей брак случился при изготовлении 
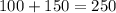деталей.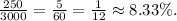
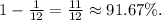
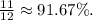
1)34.5+7.87=42.37
2)44-42.37=1.63
3)1.63:0.05=32.6
4)10.02*5=50.1
5)50.1-32.6=17.5
г)3,36:3,2+(4-(7-6,3)*4,2)-1,1=1.01
1)7-6.3=0.7
2)0.7*4.2=2.94
3)4-2.94=1.06
4)3.36:3.2=1.05
5)1.05+1.06=2.11
6)2.11-1.1=1.01