Перпендикуляр проведённый от точки к плоскости, основания перпендикуляра -
Перпендикуляром, проведённым из данной точки к данной плоскости, называется отрезок, соединяющий данную точку с точкой плоскости, и лежащий на прямой, перпендикулярной плоскости. Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра.
Теорема о трёх перпендикулярах -
прямая, проведённая в плоскости через основание наклонной перпендикулярно к её проекции на эту плоскость, перпендикулярна и к самой наклонной.
Відповідь:
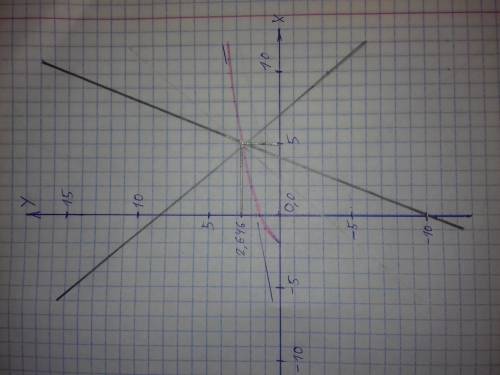
Угловой коэффициент прямой ( больший по модулю ) к = 2,856
Покрокове пояснення:
Задана функция у = sqrt ( x + 2 )
При х = 2, у = sqrt ( 5 + 2 ) = 2,646
Определим угол наклона функции в точке с координатами ( 5; 2,646 ). Вычислим значения функции в точках находящихся слева и справа на небольшом удалении это точки ( 4,99; 2,644 ) и ( 5,01; 2,648 ). При смещении х на величину 0,02, у изменяется на 0,00378.
0,00378 / 0,02 = 0,189 - это соответствует углу 10,702°.
По условиям задачи искомая прямая должна проходить через точку с координатами ( 5; 2,646 ) под углом 60° к графику функции у = sqrt ( x + 2 ), это возможно при наклоне прямой под углами
1) 10,702° + 60° = 70,702°
2) 10,702° - 60° = -49,298°
Уравнение прямой у = кх + в. Определим коэффициент наклона прямой.
1) к = tg ( 70,702 ) = 2,856
2) к = tg ( -49,298 ) = -1,163
Определим в подставив координаты точки ( 5; 2,646 ) в уравнение.
1) 2,646 = 2,856 × 5 + в
в = -11,633
Искомое уравнение имеет вид
у = 2,856 × х - 11,633
2) 2,646 = -1,163 × 5 + в
в = 8,458
Искомое уравнение имеет вид
у = -1,163 × х + 8,458