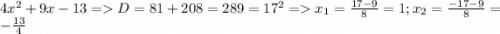du/dx=3x²y³(tg²(x³y³)+1)
d²u/dx²=6xy³(tg²(x³y³)+1)+3x²y³2(tg(x³y³)3x²y³(tg²(x³y³)+1)==6xy³(3x³y³tg(x³y³)+1)(tg²(x³y³)+1)
Аналогично
du/dy=3x3y2(tg²(x³y³)+1)
d²u/dy²=6x³y(tg²(x³y³)+1)+3x³y²2(tg(x³y³)3x³y²(tg²(x³y³)+1)==6x³y²(3x³y³tg(x³y³)+1)(tg²(x³y³)+1)
смешанные
d²u/dxdy=d(3x²y³(tg²(x³y³)+1))/dy=9x²y²(tg²(x³y³)+1)+3x²y³2tg(x³y³)3x³y²(tg²(x³y³)+1)=9x²y²(2x³y³tg(x³y³)+1)(tg²(x³y³)+1)
d²u/dydx=d(3x³y²(tg²(x³y³)+1))/dx=9x²y²(tg²(x³y³)+1)+3x³y²2tg(x³y³)3x²y³(tg²(x³y³)+1)=9x²y²(2x³y³tg(x³y³)+1)(tg²(x³y³)+1),
т.е. смешанные производные равны
ответ: x1=1 ; x2=-13/4=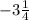
Пошаговое объяснение: