Question

Начерти равнобедреннуно трапецию, основания которой равны 4,4 см
и 6,2 см, а расстояние между ними равно 35 мм. Проведи среднюю линию этой трапеции. Получились две новые трапеции. Сделай необходимые измерения и вычисли периметры этих трапеций. На сколько
процентов периметр одной трапеции меньше периметра другой?​

Answer 1

Периметр одной трапеции на 12% меньше периметра другой.

Пошаговое объяснение:

1. Строим трапецию по условию задачи (см. рисунок).

2. Есть такое свойство равнобедренной трапеции:

Высота (CP), опущенная из вершины (C) на большее основание (AD), делит его на большой отрезок (AP), который равен полусумме оснований и меньший (PD) - равен полуразности оснований:

Нам нужен меньший отрезок (PD) ⇒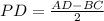 $PD=\frac{AD-BC}{2}$

Переводим длины оснований из сантиметров в миллиметры и подставляем в формулу.

⇒ $PD=\frac{62-44}{2}=\frac{18}{2}=9mm$

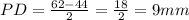
3. Рассмотрим Δ CDP - это прямоугольный треугольник.

В нём CP = 35 мм; PD = 9 мм

Применяем теорему Пифагора, и вычисляем CD:

$CD^{2} = CP^{2} + PD^{2}\\\\ CD^{2} = 35^{2} + 9^{2}\\\\ CD = \sqrt{1225+81}\\\\ CD = \sqrt{1306} \\\\ CD = AB = 36.14 mm$

4. Вычисляем длину средней линии трапеции EF по формуле:

$EF=\frac{AD+BC}{2} = \frac{62+44}{2} = \frac{106}{2} = 53 mm$

5. Т.к. средняя линия трапеции делит её боковые стороны пополам, а из-за того что трапеция равнобедренная ⇒ AB = CD

⇒ $AE = EB = CF = FD = \frac{CD}{2} = \frac{36,14}{2} = 18,07mm$

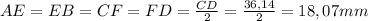
6. Вычисляем периметры трапеций BCFE и EFDA:

$P_{BCFE} = BC+EF+(2*CF)=44+53+(2*18,07) = 44+53+36,14=133,14mm$

$P_{EFDA} = EF+AD+(2*FD)=53+62+(2*18,07) = 53+62+36,14=151,14mm$

7. Вычисляем процентную разницу между периметрами трапеций BCFE и EFDA:

Для начала составляем пропорцию:

Если P(EFDA) ⇒ 100%

То P(BCFE) ⇒ x%

Находим x:

$x=\frac{P_{BCFE}*100}{P_{EFDA}} = \frac{133,14*100}{151,14} = 88$

⇒ Процентная разница = 100% - 88% = 12%