Объем полной поверхности правильной шестиугольной призмы равен 415,7 см3, а площадь 323,1 см2.
Пошаговое объяснение:
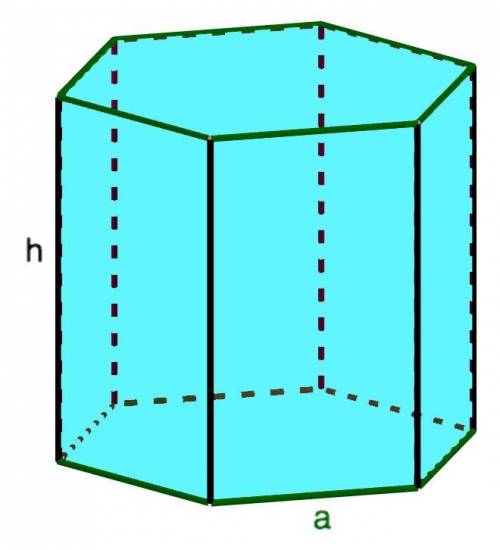
У правильной шестиугольной призмы основанием является правильный шестиугольник, где боковые грани перпендикулярны основаниям.
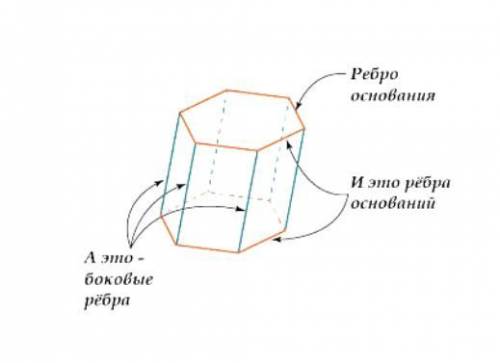
Объем правильной шестиугольной призмы равен произведению площади правильного шестиугольника, лежащего в основании, на высоту призмы, где высота призмы - это её боковое ребро.
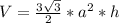
У нас боковое ребро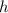 
равно 10 см, а ребро основания 
равно 4 см (как наглядно показано на рисунке). Подставляем и считаем:
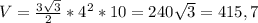см3.
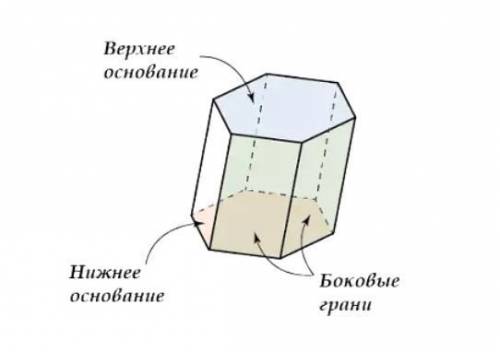
Правильная шестиугольная призма имеет два основания, где ее основания - правильные шестиугольники со стороной , и шесть боковых сторон, которые представляют из себя прямоугольники со сторонами и .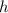
Поэтому площадь полной поверхности правильной шестиугольной призмы равна сумме площадей ее двух оснований и шести площадей боковых граней призмы.
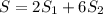
Где площадь основания находится согласно формуле:
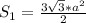
А площадь боковых граней равна: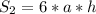 
Подставляя это в формулу общей площади получим:
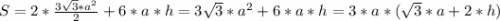
Подставляя наши значения получаем:
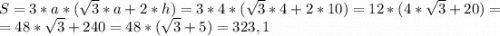см2.
Получаем ответ: объем полной поверхности правильной шестиугольной призмы равен 415,7 см3, а площадь 323,1 см2.
Пошаговое объяснение:
Нам нужно упростить заданное выражение 1/2а + 1/3а - 1/4а и найти его значение при а = 1 5/7.
Чтобы упростить выражение вспомним определение подобных слагаемых и как их привести.
Слагаемые, имеющие одинаковую буквенную часть, называют подобными слагаемыми.
Чтобы сложить (привести) подобные слагаемые, надо сложить их коэффициенты и результат умножить на общую буквенную часть.
1/2а + 1/3а - 1/4а = а(1/2 + 1/3 - 1/4) = а(6/12 + 4/12 - 3/12) = а((6 + 4 - 3)/12) = 7/12а.
Найдем значение выражения при а = 1 5/7:
7/12 * 1 5/7 = 7/12 * 12/7 = 1.
ответ: 7/12а; при а = 1 5/7 значение выражения равно 1.
а) ответом на этот пример будет отношение коэффициентов при старших степенях переменной числителя и знаменателя, поскольку в числителе и знаменателе - стандартные многочлены 4-й степени и х стремится к ∞; 8/2=4
б)Разложим предварительно многочлены на линейные множители.
3х²+5х-42=0; х₁,₂=(-5±√(25+3*4*42) )/6=(-5±√529)/6=(-5±23)/6; х₁=3; х₂=-14/3; 3х²+5х-42=3*(х-3)(х+14/3)=(х-3)(3х+14); х²-5х+6=0, по теореме, обратной теореме Виета х₁=2; х₂=3; х²-5х+6=(х-2)(х-3). Разделим числитель на знаменатель, с учетом разложений.
(3х²+5х-42)/(х²-5х+6)=(х-3)(3х+14)/(х-2)(х-3)=(3х+14)(х-2). предел от (3х+14)(х-2) при х стремящемся к 3, равен (3*3+14)(3-2)=9+14=23
в) разложение числителя х²-3х+2 , предварительно с подсчитанными по теореме, обратной теореме Виета корнями уравнения х²-3х+2=0, х₁=1; х₂=2, примет вид х²-3х+2=(х-1)*(х-2). Домножим числитель и знаменатель на скобку (√(5-х)+√(х+1)), сопряженную знаменателю. В знаменателе вырисовалась разность квадратов (а-в)*(а+в)=а²-в², т.е. (5-х)-(х+1)=5-х-х-1=4-2х=-2*(х-2), а числитель примет вид
(√(5-х)+√(х+1))*(х-1)(х-2). После деления числителя на знаменатель получим
((√(5-х)+√(х+1))*(х-1)(х-2))/(-2*(х-2))=-((√(5-х)+√(х+1))*(х-1))/(2*(х-1)), подставим вместо х=2, получим -(√3+√3)(2-1)/(2*(2-1))=-2√3/2=-√3
В основании правильной шестиугольной призмы с высотой 10 см лежит шестиугольник со стороной 4 см.
1) Найдем площадь полной поверхности:
S п.п. = 3а • (а√3 + 2h)
S п.п. = 3•4 • (4√3 + 2•10) =
= 12 • (4√3 + 20) = 323,138 кв.см
2) Найдем объем правильной шестиугольной призмы.
V = (h√3)•(3а²)/2
где h - высота, а - сторона равностороннего шестиугольника в основании.
V = (10√3)•(3•4²)/2 =
= 240√3 = 415,692 куб.м.