Question

Пароль состоит из 4 цифр .Замок откроется , если ввести правильные 4 цифры в любом порядке. В пароле необязательно все цифры разные.Гоша пробует разные пароли.Какова вероятность того,что замок откроется за первые три попытки ? Записать ответ в виде обыкновенной дроби

Answer 1

По условию задачи нужно угадать не сам пароль (число), а комбинацию цифр, из которых можно это число составить. Под числом будем понимать упорядоченную последовательность четырех цифр от 0000 до 9999 (то есть в отличие от четырехзначного числа впереди могут стоять нули).

Для начала разделим все числа на группы:

1. Группа чисел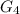 $G_{4}$ , состоящих из четырех одинаковых цифр.

2. Группа чисел $G_{31}$, состоящих из трех одинаковых цифр и еще одной другой цифры.

3. Группа чисел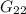 $G_{22}$, состоящих из двух пар одинаковых, но разных между собой цифр.

4. Группа чисел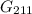 $G_{211}$, состоящих из двух одинаковых цифр и еще из двух двух других и разных между собой цифр.

5. Группа чисел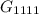 $G_{1111}$, состоящих из разных одинаковых цифр.

Определим число чисел в группа и число соответствующих им комбинаций.

1. Рассмотрим группу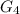 $G_{4}$. Количество чисел, состоящих из четырех одинаковых цифр, равно 10.

$N_{4}=10$

Заметим, что для каждого такого числа есть только одна комбинация получить это число. То есть и количество комбинаций в этом случае совпадает с количеством чисел:

$K_{4}=N_{4}=10$

2. Рассмотрим группу $G_{31}$. Определим количество чисел в этой группе. Первую цифру мы можем выбрать , вторую цифру , а также еще мы можем разместить в числе уникальную цифру. Таким образом, общее количество чисел:

$N_{31}=10\cdot9\cdot4=360$

Но поскольку положение уникальной цифры в числе для комбинации безразлично, а таких положений в числе 4, то количество комбинаций в 4 раза меньше:

$K_{31}=\dfrac{N_{31}}{4} =90$

3. Рассмотрим группу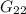 $G_{22}$. Определим количество чисел в этой группе. Первую цифру мы можем выбрать , вторую  цифру . Еще мы можем разместить в числе одну пару чисел, тогда другая размещается автоматически (это места 12, 13, 14). Таким образом, общее количество чисел:

$N_{22}=10\cdot9\cdot3=270$

Заметим, что 6 числам вида ААВВ, АВАВ, АВВА, ВВАА, ВАВА, ВААВ соответствует одна комбинация. То есть, количество комбинаций в 6 раза меньше:

$K_{22}=\dfrac{N_{22}}{6} =45$

4. Рассмотрим группу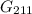 $G_{211}$. Определим количество чисел в этой группе. Первую цифру мы можем выбрать , вторую  цифру , третью цифру . Еще мы можем разместить в числе повторяющуюся пару чисел, и еще мы можем разместить на свободные места оставшиеся две цифры. Таким образом, общее количество чисел:

$N_{211}=10\cdot9\cdot8\cdot3\cdot2=4320$

Проводя аналогию с предыдущим пунктом, можно понять, что одной комбинации соответствует уже 12 чисел. Чтобы это понять, можно в перечисленных в предыдущем пункте числам вместо цифр (В, В) подставлять сначала цифры (C, D), а затем (D, C) именно в таком порядке. Итак, количество комбинаций в 12 раза меньше:

$K_{211}=\dfrac{N_{211}}{12} =360$

5. Наконец, рассмотрим группу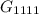 $G_{1111}$. Определим количество чисел в этой группе. Первую цифру мы можем выбрать , вторую  цифру , третью цифру , четвертую цифру . Тогда, общее количество чисел:

$N_{1111}=10\cdot9\cdot8\cdot7=5040$

Заметим, что одна комбинация соответствует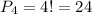 $P_4=4!=24$ числам. То есть, количество комбинаций в 24 раза меньше:

$K_{1111}=\dfrac{N_{1111}}{24} =210$

Находим общее число комбинаций:

$K=K_4+K_{31}+K_{22}+K_{211}+K_{1111}=10+90+45+360+210=715$

По условию, у нас есть 3 попытки отгадать комбинацию. Значит, вероятность того, что замок откроется за первые три попытки:

$P(A)=\dfrac{3}{715}$

ответ: 3/715

Дополнение. Определять количество комбинаций по имеющемуся количеству чисел очень удобно с перестановок с повторениями:

$P_n^{n_1,n_2,...,n_m}=\dfrac{n!}{n_1!\ n_2!\ ...\ n_m!}$

В частности, нижние индексы групп становятся верхними индексами в формуле перестановок с повторениями.

Еще раз краткое решение в формулах:

$N_{4}=A_{10}^1;\ K_{4}=\dfrac{N_{4}}{P_4^4} =10$

$N_{31}=A_{10}^2\cdot C_4^1=360;\ K_{31}=\dfrac{N_{31}}{P_4^{3,1}} =90$

$N_{22}=A_{10}^2\cdot C_4^2=270;\ K_{22}=\dfrac{N_{22}}{P_4^{2,2}} =45$

$N_{211}=A_{10}^3\cdot C_4^2\cdot P_2=4320;\ K_{211}=\dfrac{N_{211}}{P_4^{2,1,1}} =360$

$N_{1111}=A_{10}^4=5040;\ K_{1111}=\dfrac{N_{1111}}{P_4} =210$

$P(A)=\dfrac{3}{\Sigma K} =\dfrac{3}{715}$

ответ: 3/715