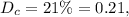 а долю масла в сливках, как
а долю масла в сливках, как 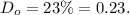
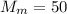 кг молока. Посчитаем, какую массу масла
кг молока. Посчитаем, какую массу масла 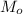 можно из него получить.
можно из него получить.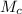 , которую можно собрать с молока, воспользуемся простым правилом: умножаем на число процентов в доле и делим на сто процентов:
, которую можно собрать с молока, воспользуемся простым правилом: умножаем на число процентов в доле и делим на сто процентов: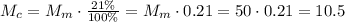 кг.
кг.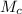 мы просто умножили
мы просто умножили 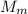 на
на 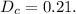
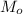 , которую можно выделить из собранных сливок, воспользуемся теми же правилами:
, которую можно выделить из собранных сливок, воспользуемся теми же правилами: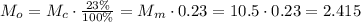 кг масла
кг масла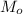 мы просто умножили
мы просто умножили 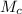 на
на 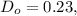 т.е., учитывая расчёт **(A)** мы умножили
т.е., учитывая расчёт **(A)** мы умножили 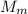 на
на 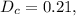 а затем на
а затем на 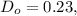 и в самом деле:
и в самом деле: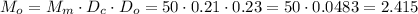 кг масла
кг масла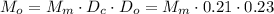 ;
;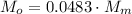 ;
;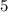 кг
кг 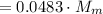 ;
;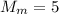 кг
кг 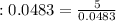 кг
кг 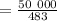 кг ;
кг ;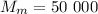 кг
кг 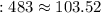 кг ;
кг ;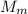 из уравнения **(С)** :
из уравнения **(С)** :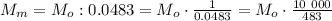 и опять же найдем, что:
и опять же найдем, что: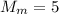 кг
кг 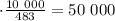 кг
кг 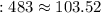 кг ;
кг ;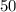 кг молока можно получить
кг молока можно получить 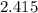 кг масла.
кг масла.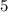 кг масла нужно
кг масла нужно 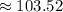 кг молока.
кг молока.
ответ: a<-3.
Пошаговое объяснение:
знайдіть, при яких значеннях а рівняння x² + (a + 1)x + 1 = 0 не має дійсних коренів
x² + (a + 1)x + 1 = 0;
a=1; b=(a+1); c=1;
D=b²-4ac=(a+1)²-4*1*1= (a+1)²-4;
Уравнение не имеет действительных корней когда дискриминант отрицательный (D<0).
(a+1)²-4<0;
(a+1)²<4;
a+1<±2;
a<2-1;
a1<1;
a<-2-1;
a<-3.