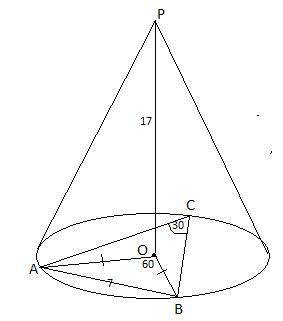
Вписанный угол 30 в основание конуса опирается на дугу. Хорда длинной 7 стягивает эту дугу. Высота конуса 17. Найти площадь полной поверхности конуса.
Пошаговое объяснение:
Дуга ∪АВ=60° ( вписанный угол равен половины дуги на которую опирается). Значит центральный угол ∠АОВ=60°.
Т.к. ОА=ОВ , то ΔАОВ равнобедренный .Т.к. ∠АОВ=60° , значит ∠А=∠В=(180°-60°):2=60° ⇒ ΔАОВ-равносторонний и АВ=ОВ=7 ⇒r=7
ΔАОР-прямоугольный, по т. Пифагора РА=√(17²+7)²= √338=13√2.
РА-образующая конуса.
S(полное)= S(круга)+ S(бок),
S(круга)= π r² , S(круга)= π *7²=49π.
S(бок.кон. )=π * r* l , S(бок.кон. )= π *7*13√2=91√2 π
S(полное)= 49π+91√2 π (ед²)
Пошаговое объяснение:
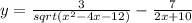
в данном случае ООФ функции определяется условиями
1. знаменатель ≠ 0
2.подкоренное выражение > 0 (строго больше 0 т.к. корень в знаменателе
1. 2х+10 ≠0; х ≠-5
x²-4x-12 >0
сначала найдем нули функции
f(x)=x²-4x-12 =0 ⇒ х₁ = -2; х₂ = 6 это точки смена знака функции
получили три промежутка
(-∞; -2); (-2;6); (6;+∞)
точка х= -5 попадает в промежуток (-∞; -2) будем иметь ее в виду
итак промежуток
(-∞; -2); f(-3) = 9 > 0
(-2;6); f(0) = -12 < 0
(6;+∞); f(7) = 9 > 0
теперь вспоминаем, что для первичной функции у есть условие х≠-5,
поэтому получаем
ООФ:
х ∈ (-∞; -5) ∪ (-5;-2) ∪ (6;+∞)