Вообще говоря, эту задачу можно решать с метода множителей Лагранжа, но я постараюсь обойтись без них. Задача максимизировать произведение abc трех положительных чисел при условии постоянства суммы a²+b²+c² их квадратов. Понятно. что вместо произведения чисел можно рассмотреть произведение их квадратов, а обозначив их буквами x, y, z соответственно, получаем более симпатичную формулировку: максимизировать произведение xyz положительных чисел при условии x+y+z=K (K - некоторое положительное число).
Как всегда в таких задачах, ищем точки, в которых обе частные производные равны нулю (иными словами, точки, в которых первый дифференциал равен нулю):
Сокращение на x и y оправдано их положительностью. (Кстати, если даже попробовать представить себе параллелепипед с нулевой стороной, шансов у такого вырожденца иметь наибольший объем нет никаких.) Далее теория советует исследовать второй дифференциал в найденных критических точках на положительную или отрицательную определенность с критерия Сильвестра. Давайте последуем этим советам.
Видим, что угловой минор первого порядка -2K/3<0; угловой минор второго порядка K²/3>0. Значит, второй дифференциал отрицательно определен, а это в условиях равенства нулю дифференциала первого порядка означает наличие точки максимума.
Итак, доказано, что наибольший объем среди параллелепипедов с фиксированной диагональю имеет куб.
Краткая запись: Купили вишнёвого сока - 4 пакeта. С (стоимость) 1-го пакeта - 130 т. (тeнгe) С (стоимость) конфeт - ? т. Заплатили за всю покупку - 1.100 т.
Аист:здравствуй друг мои зеленый Лягушка: здравствуй друг мой пернатый,как жизнь,как мир поведал? Аист:ой друг мой,расскажут так и быть. Повидал я многих неведомых зверюшек, интересных и страшных,Повидал я столицы старые,древние,Повидал я жизнь неземную,сколько красок в этом мире творится! Лягушка: и в правду,на свете столько много зверей! от белых до черных,от малых до больших. Аист,ты нашел новых друзей и кто они? Аист: Много я видел,многих я знал! Мне больше всего запал Кемгуру! представь Лягушка, большой,красивый,необычный,бойкий,быстрый-чудозверь. Поверь ты никогда не видел столь чудного зверька!Как же матушка природа одарила этот мир. Мне по нраву этот зверь, я завел с ним диалог,но знай язык он мой не понимал. И пришлось мне наблюдать за ним.Но ничего,таких я редко где увижу,поговорить не удалось зато открытие я сделал для себя!
Вообще говоря, эту задачу можно решать с метода множителей Лагранжа, но я постараюсь обойтись без них. Задача максимизировать произведение abc трех положительных чисел при условии постоянства суммы a²+b²+c² их квадратов. Понятно. что вместо произведения чисел можно рассмотреть произведение их квадратов, а обозначив их буквами x, y, z соответственно, получаем более симпатичную формулировку: максимизировать произведение xyz положительных чисел при условии x+y+z=K (K - некоторое положительное число).
Как всегда в таких задачах, ищем точки, в которых обе частные производные равны нулю (иными словами, точки, в которых первый дифференциал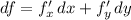 равен нулю):
равен нулю):
Видим, что угловой минор первого порядка -2K/3<0; угловой минор второго порядка K²/3>0. Значит, второй дифференциал отрицательно определен, а это в условиях равенства нулю дифференциала первого порядка означает наличие точки максимума.
Итак, доказано, что наибольший объем среди параллелепипедов с фиксированной диагональю имеет куб.