Question

Упростить:

Только задание 1.1

Answer 1

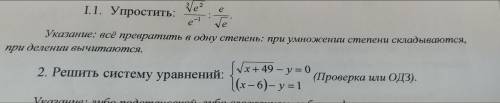
$\\ \frac{ \sqrt[3]{e {}^{2} } }{e {}^{ - 1} } \div \frac{e}{ \sqrt{e} } = \frac{ \sqrt[3]{e {}^{2} } }{e {}^{ - 1} } \times \frac{ \sqrt{e} }{e} = \frac{ \sqrt[3]{e { {}^{} }^{2} } {}^{} \sqrt{e} }{e {}^{ - 1 + 1} } = \frac{ \sqrt[3]{e {}^{2} } \sqrt{e} }{1} = \sqrt[6]{e {}^{4} } \sqrt[6]{e {}^{3} } = \sqrt[6]{e {}^{4} \times e {}^{3} } = \sqrt[6]{e {}^{4 + 3} } = \sqrt[6]{e {}^{7} } = \sqrt[6]{e {}^{6} \times e} = \sqrt[6]{e {}^{6} } \sqrt[6]{e} = e \sqrt[6]{e} \\ \\ otvet : \: \: \: e \sqrt[6]{e}$

Answer 2

$\displaystyle\ \frac{\sqrt[3]{e^2} }{e^{-1}} :\frac{e}{\sqrt{e} } =\frac{\sqrt[3]{e^2} }{\frac{1}{e} } \cdot \frac{\sqrt{e} }{e} =\sqrt[3]{e^2} \cdot e\cdot\frac{\sqrt{e} }{e} = \sqrt[3]{e^2} \cdot\sqrt{e} =e^\frac{2}{3} \cdot e^\frac{1}{2} =e^{\frac{2}{3} +\frac{1}{2} }=e^\frac{7}{6} =\boxed{e\sqrt[6]{e} }$