V фигуры = 224π см³ ≈ 703 см³
Пошаговое объяснение:
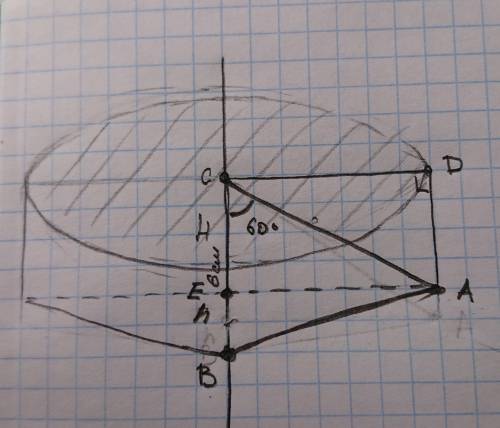
Данную фигуру можно разделить на цилинд и конус.
Проведём высоту треугольника ABC из угла A к основанию BC. Пересечение с BC отметим как точку E (см рисунок)
Тогда прямоугольник ACED при вращении образует цилиндр, а треугольник ABE - конус
Радуиусы фигур будут одинаковыми
R = 8*Sin 60° = 8*√3/2 = 4*√3 см
Высота цилиндра H = 8*Cos 60° = 8*1/2 = 4 см
Высота конуса h = CB - h = 6 - 4 = 2 см
V цилиндра = π*R²*H = π * 4² *3*4 = 192π см³
V конуса = 1/3π*R²*h = π * (1/3) * 4² * 3 * 2 = 32π см³
V фигуры = Vц + Vк = 224π см³ ≈ 703 см³
ответ:На рисунке дана треугольная пирамида с ребром DA , перпендикулярным основанию.
piramida.JPG
DA — перпендикулярное основанию ребро, DA также является высотой,
Δ DAC и Δ DAB — прямоугольные, угол DEA — двугранный угол при основании.
На следующем рисунке дана пирамида, основание которой — прямоугольник.
PERPENDIKULARA SKAUTNE 2.JPG
Ребро SB перпендикулярно основанию, SB также является высотой,
Δ SBA и Δ SBC — прямоугольные;
если основание — прямоугольник, то Δ SAD и SCD — прямоугольные.
Пример:
в задании это нужно доказывать при теоремы о трёх перпендикулярах ТТП — прямая, которая проведена на плоскости через основание наклонной перпендикулярно её проекции на эту плоскость, перпендикулярна и самой наклонной.
Если прямая AD перпендикулярна проекции наклонной AB , то она перпендикулярна и наклонной SA .
Если прямая CD перпендикулярна проекции наклонной BC , то она перпендикулярна и наклонной SC .
PERPENDIKULARA SKAUTNE 3.JPG
Записываем с символов:
AD⊥AB,т.к. основание − прямоугольникSB⊥AB,т.к. высота}⇒AD⊥SA ,
значит, ∢ SAD= 90° и Δ SAD — прямоугольный.
Подобным образом доказывается, что Δ SCD — прямоугольный:
CD⊥BC,т.к. основание − прямоугольникSB⊥BC,т.к. высота}⇒CD⊥SC
Пошаговое объяснение:
Пошаговое объяснение:
1. Найти радианную меру угла равного:
a) 40° => α рад=π*α°/180°=40°π/180°=0.2π≈0.7 радиан;
б) 120° => 120°π/180°=2/3π≈2.1 радиан;
в) 105° => 105°π/180°= 7/12π=1.8 радиан;
г) 60° => 60°π/180°=π/3=1 радиан;
д) 45°=> 45°π/180°=π/4=0.79 радиан;
е) 360° => 360°π/180°=2π=6.28 радиан;
***
2. Найти градусную меру угла выраженного в радианах:
а) 5П/4 => 5π/4 *180°/π=225°;
б) П/9 => π/9*180°/π=180/9=20°;
в) 2*П/3 => 2π/3*180/π=120°;
***
3. Вычислить:
а) log₅5 = 1;
б) log6 216 =3;
в) log10/3 0,09 = -2.