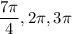
а)
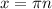
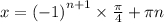
n∈Z
б)
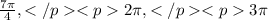
Пояснение:
№13(а)
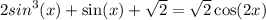
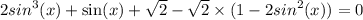
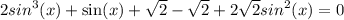
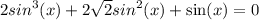
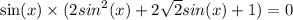
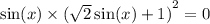
Произведение равно нулю,когда хотя бы один из множителей равен нулю
1)
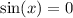
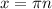
n∈Z
2)
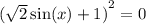
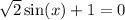
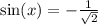

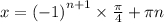
n∈Z
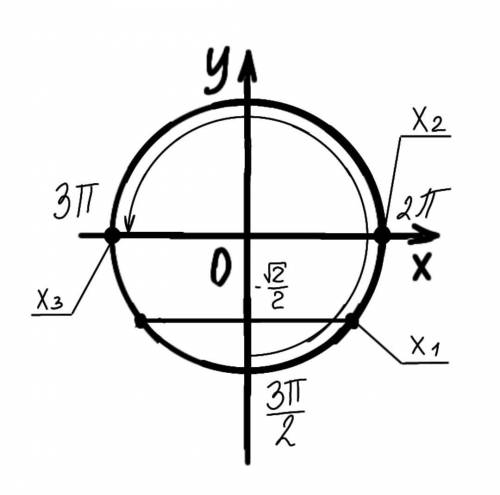
б) Найдем корни уравнения,принадлежащие отрезку [3п/2;3п], с тригонометрической окружности(см. вложение)
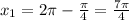
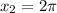
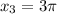
Пошаговое объяснение:
Известно, что СД = 18 см, СК = 14 см и ВД = 12 см, причем точки К и В лежат на отрезке СД.
Необходимо вычислить длину отрезка ВК.
Поскольку СК > ВД, это значит, что точка В лежит между точками С и К.
Составим выражение для определения длины отрезка СД.
СД = СВ + ВК + КД.
Теперь представим в виде выражения длину отрезка СК.
СК = СВ + ВК.
СВ = СК – ВК.
Преобразуем выражение, представляющее длину отрезка ВД.
ВД = ВК + КД.
КД = ВД – ВК.
Подставим полученные значения в выражение СД = СВ + ВК + КД.
СД = СК – ВК + ВК + ВД – ВК.
ВК = СК + ВД – СД.
Подставим значения, известные из условий задания.
ВК = 14 + 12 – 18.
ВК = 8 см.
ответ: длина отрезка ВК = 8 см.
а)
б)
Пошаговое объяснение:
а)
б) Отберём корни с тригонометрической окружности (см. рис.)
Подходят корни