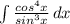 . ответ должен получиться:
. ответ должен получиться: 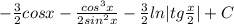
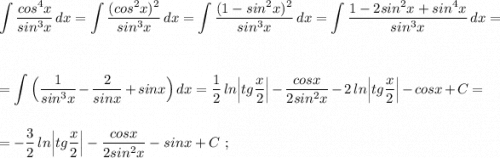
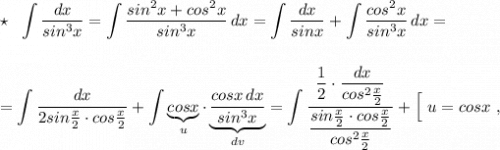
![\displaystyle du=-sinx\, dx\ ,\ dv=\frac{cosx\, dx}{sin^3x}\ ,\ v=\int (sinx)^{-3}\cdot d(sinx)=-\frac{1}{2\, sin^2x}\Big]=\\\\\\=\int \frac{d(tg\frac{x}{2})}{tg\frac{x}{2}}-\frac{cosx}{2sin^2x}-\int \frac{sinx\, dx}{2sin^2x}=ln\Big|tg\frac{x}{2}\Big|-\frac{cosx}{2sin^2x}-\frac{1}{2}\int \frac{dx}{sinx}=\\\\\\=ln\Big|tg\frac{x}{2}\Big|-\frac{cosx}{2sin^2x}-\frac{1}{2}\cdot ln\Big|tg\frac{x}{2}\Big|+C=\frac{1}{2}\cdot ln\Big|tg\frac{x}{2}\Big|-\frac{cosx}{2sin^2x} +C\ \ \ \star](/tpl/images/2007/8890/b8205.png)
Периметр прямоугольника по формуле: Р = 2*(a+b).
Рисунок к задаче в приложении.
ДАНО: a = 4 м, b = 3 м, c = 3 м.
РЕШЕНИЕ
Из рисунка видно, что можно применить два варианта расчёта.
Вариант 1. Сумма периметров двух пар стен.
Р₁ = 2*(a+b) = 2*(4+3) = 14 м - периметр длинной стены.
Р₂ = 2*(b+c) = 2*(3+3) = 12 м - периметр короткой стены.
Р = 2*(Р₁+Р₂) = 2*(14+12) = 52 м - периметр стен - ОТВЕТ 1
Вариант 2. Сумма длин всех рёбер прямоугольника плюс 4 длины высоты стен.
Формула суммы длин рёбер параллелепипеда:
P₁ = 4*(a+b+c) = 4*(4+3+3) = 4*10 = 40 метров
Р = Р₁ + 4*b = 40 + 4*3 = 40+12 = 52 м - периметр - ОТВЕТ 2
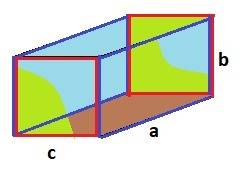
Периметр прямоугольника по формуле: Р = 2*(a+b).
Рисунок к задаче в приложении.
ДАНО: a = 4 м, b = 3 м, c = 3 м.
РЕШЕНИЕ
Из рисунка видно, что можно применить два варианта расчёта.
Вариант 1. Сумма периметров двух пар стен.
Р₁ = 2*(a+b) = 2*(4+3) = 14 м - периметр длинной стены.
Р₂ = 2*(b+c) = 2*(3+3) = 12 м - периметр короткой стены.
Р = 2*(Р₁+Р₂) = 2*(14+12) = 52 м - периметр стен - ОТВЕТ 1
Вариант 2. Сумма длин всех рёбер прямоугольника плюс 4 длины высоты стен.
Формула суммы длин рёбер параллелепипеда:
P₁ = 4*(a+b+c) = 4*(4+3+3) = 4*10 = 40 метров
Р = Р₁ + 4*b = 40 + 4*3 = 40+12 = 52 м - периметр - ОТВЕТ 2
