Question

Если x;y;z действительные числа то найдите x+y+z если известно $\displaystyle\bf \\\begin{equation*} \begin{cases} x(yz-1) = 712 \\ y(xz-1)=711 \\ z(xy-1) = 710 \end{cases}\end{equation*}$

Answer 1

(см. объяснение)

Пошаговое объяснение:

$\begin{equation*} \begin{cases} x(yz-1)=712 \\ y(xz-1)=711 \\ z(xy-1)=710 \end{cases}\end{equation*}$

1) Вычитаем из первой строки системы вторую: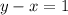 $y-x=1$

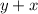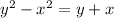
   Умножаем полученное на $y+x$: $y^2-x^2=y+x$

2) Вычитаем из первой строки системы третью: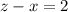 $z-x=2$

   Умножаем полученное на $z+x$: $z^2-x^2=2z+2x$

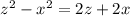
3) Вычитаем из второй строки системы третью: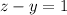 $z-y=1$

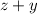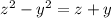
   Умножаем полученное на $z+y$: $z^2-y^2=z+y$

Складываем полученное в пунктах 1 и 3: $z^2-x^2=x+2y+z$

Приравниваем к полученному в пункте 2: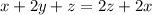 $x+2y+z=2z+2x$

Упрощаем только что выведенное выражение: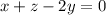 $x+z-2y=0$

Выражаем x+z: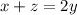 $x+z=2y$

Тогда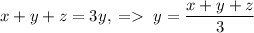 $x+y+z=3y,\;=\;y=\dfrac{x+y+z}{3}$.

Пусть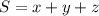 $S=x+y+z$. В этом случае $y=\dfrac{S}{3}$.

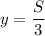Возвращаясь к записям в пунктах 1 и 3, получаем x и z через S:

$x=y-1,\;=\;x=\dfrac{S}{3}-1$

$z=y+1,\;=\;z=\dfrac{S}{3}+1$

Теперь сложим все три строки исходной системы.

Раскрыв скобки и приведя подобные, получим:

$3xyz-(x+y+z)=2133\\3xyz-S=2133$

Подставляем выведенные выше x, y и z в это уравнение:

$3\left(\dfrac{S}{3}-1\right)\times\dfrac{S}{3}\times\left(\dfrac{S}{3}+1\right)-S=2133\\S\times\left(\dfrac{S}{3}-1\right)\times\left(\dfrac{S}{3}+1\right)-S=2133$

Таким образом, мы все свели к уравнению, в котором есть только одна неизвестная, причем та, которую мы ищем.

Решив его, находим, что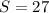 $S=27$.

Задание выполнено!

Answer 2

27

Пошаговое объяснение:

Можно просто в "лоб" решать, найдя x,y и z