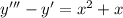
Задача 1: Параллелепипед имеет длину а = 16 см., ширину b = 3 см. и высоту с = 2 см. Найдите объем параллепипеда.
V = a * b * c = 16 * 3 * 2 = 96 см²
Задача 2: Параллелепипед имеет длину а = 9 дм и ширину b = 7 дм. Объем равен 630 дм². Найдите высоту параллепипеда.
V = a * b * c
с = V / a * b =630 / 63 = 10 дм.
Задача 3: Параллелепипед имеет длину а = 5 м. и высоту с = 4 м. Объем равен 80 м². Найдите ширину параллепипеда.
V = a * b * c
b = V / a * c = 80 / 20 = 4 м.
Задача 4: Параллелепипед имеет ширину b = 8 мм. и высоту с = 3 мм. Объем равен 96 мм². Найдите длину параллепипеда.
V = a * b * c
a = V / b * c = 96 / 24 = 4 мм.
1110 м - длина тоннеля
Пошаговое объяснение:
Первый вагон поезда уже проехал весь поезд , когда последний ваго только на него въехал , значит первый вагон проехал путь равный длине моста и своей собственной длине
750 + 510 = 1260 м
Скорость была :
1 мин = 60 с
1 мин 10 с = 70 с
1260м : 70 = 18 м/с
Значит за 1,5 минуты поезд
1,5 мин= 90 с
18м/с * 90с = 1620 м - это будет длина тоннеля и поезда вместе
значит длина тоннеля будет равна разнице между расстоянием которое поезд за 1,5 мин и длиной поезда:
1620 - 510 = 1110м
Відповідь:
Покрокове пояснення:
Cоставляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r^3 - r = 0
Вынесем r за скобку. Получим:
r(r^2-1) = 0
Здесь r1 = 0. Найдем остальные корни.
r^2 +0 r - 1 = 0
D=02 - 4·1·(-1)=4
Корни характеристического уравнения:
r1 = -1
r2 = 0
r3 = 1
Следовательно, фундаментальную систему решений составляют функции:
y1 = e^(-x)
y2 = e^(0x)
y3 = e^x
Общее решение однородного уравнения имеет вид:
y- = C1*e^(-x) +C2 +C3*e^x , Ci ∈ R
Правая часть P(x) = x^2+x, Q(x) = 0, α = 0, β = 0.
Следовательно, число α + βi = 0i является корнем характеристического уравнения кратности k = 1(r2).
Уравнение имеет частное решение вида:
y· = x (Ax^2 + Bx + C)
Вычисляем производные:
y' = A·x^2+B·x+C+x(2·A·x+B)
y'' = 2(3·A·x+B)
y''' = 6·A
которые подставляем в исходное дифференциальное уравнение:
y''' -y' = (6·A) -(A·x^2+B·x+C+x(2·A·x+B)) = x^2+x
или
-3·A·x^2+6·A-2·B·x-C = x^2+x
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
x^2: -3A = 1
1: 6A -C = 0
x: -2B = 1
Решая ее, находим:
A = -1/3;B = -1/2;C = -2;
Частное решение имеет вид:
y·=x (-1/3x^2 -1/2x -2)
Таким образом, общее решение дифференциального уравнения имеет вид:
y = y- + y. =C1*e^(-x) +C2 +C3*e^x -1/3x^3 -1/2x^2 -2x