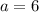 м
м
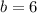 м
м
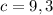 м
м
1) 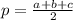 - формула полупериметра треугольника.
- формула полупериметра треугольника.
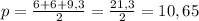 м
м
2) 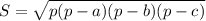 - формула площади треугольника.
- формула площади треугольника.
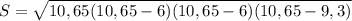
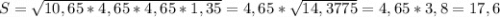
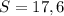 м²
м²
ответ: 17 м²
ответ: 1) dz=e^(x/y)*dx/y-x*e^(x/y)*dy/y²; 2) функция имеет максимум в точке M(2/3; 1/3).
Пошаговое объяснение:
1) z=e^(x/y)
Находим частные производные:
dz/dx=1/y*e^(x/y), dz/dy=-x/y²*e^(x/y).
Полный дифференциал dz=dz/dx*dx+dz/dy*dy=e^(x/y)*dx/y-x*e^(x/y)*dy/y²
2) Находим первые частные производные:
dz/dx=2*y+2*x-2; dz/dy=2*x+8*y-4.
Приравнивая их к нулю, получаем систему уравнений:
x+y-1=0
x+4*y-2=0
Решая её, находим x=2/3, y=1/3 - координаты единственной критической точки М(2/3; 1/3).
Находим вторые частные производные:
d²z/dx²=2; d²z/dxdy=2; d²z/dy²=8. Так как они суть постоянные числа, то и в критической точке они будут иметь те же значения:
A=d²z/dx²(M)=2; B=d²z/dxdy(M)=2; C=d²z/dy²(M)=8.
Так как выражение A*C-B²=2*8-4=12>0, то есть положительно, то в точке М функция действительно имеет экстремум. А так как при этом A=2>0, то этот экстремум является максимумом.
Пошаговое объяснение:
если известно 3 стороны , можно найти площадь треугольника по формуле Герона
S = √p*(p-a)*(p-b)*(p-c) где p - полупериметр
p = (a + b + c)/2
p = (6 + 6 + 9,3)/2
p = 10,65 м
S = √10,65*(10,65-6)*(10,65-6)*(10,65-9,3)
S = √10,65*4,65*4,65*1,35
S = √310,87749375
S = 17,63171840037153 м² ≈ 17,6 м²