В соревновании участвовало:
5 финнов;
1 норвежец;
6 шведов.
Пошаговое объяснение:
Пусть у нас
х финнов
у норвежцев
z шведов
Тогда получаем систему:
х + у + z = 12. (1)
2х + 0,5у + 0,25z = 12. (2)
вычтем из 2 уравнения 1
x-0,5y-0,75z=0
вычтем из (1) полученное уравнение,
тем самым уберем х
1,5y+1,75z=12
6y+7z=48
z может быть от 1 до 6, причём такое, при котором 6у=48-7z,или у=(48-z)/6
то есть (48-7z) кратно 6.
z = 1; 2; 3 ; 4 ; 5 - не подходят условию.
z=6 - подходит, при этом:
z=6
y=(48-7z)/6
или
z=6
y=1
Отсюда
х=12-6-1
х=5
Значит в соревновании участвовало:
5 финнов
1 норвежец
6 шведов
Проверяем по улову:
5*2 + 1*0,5 + 6*0,25 =
= 10 + 0,5 + 1,5 = 12
Все решено верно.
Что мы будем использовать: последовательность 
монотонно возрастает и имеет конечный предел; этот предел обозначается буквой e. Первые цифры числа e все знают. Для нас достаточно знать, что
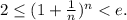
1) 
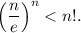При n=1 неравенство очевидно. Предположим, что оно справедливо при некотором n, и докажем, что тогда оно справедливо при n+1. Итак, нужно доказать, что 
Имеем:
2) 
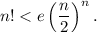При n=1 неравенство очевидно. Предположив, что при некотором n неравенство справедливо, докажем, что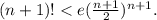 
Имеем:
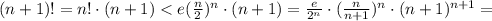
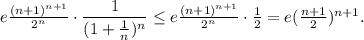
Доказательство завершено благодаря тому, что все натуральные числа расположены "по порядку" одно за другим, и есть первое натуральное число (принцип домино: если доминошки расположить на боку одну рядом с другой на небольшом расстоянии друг от друга в виде змеи, и уронить первую доминошку на вторую, то вторая упадет на третью, третья на четвертую и так далее, пока не упадут все).
3(2соs^2x-1)+cosx-4=0
6cos^2x-3+cosx-4=0
6cos^2x+cosx-7=0
cosx=y
6y^2+y-7=0
D=1+168=169
y1=(-1+13)/12=1
y2=(-1-13)/12=-14/12(не подходит)
соsx=1
x=π/2+πn n€Z
n=0 x=π/2
n=1. x=3π/2
χ=2 χ=5π/2
-3π/2×2π+1=-6π^2+1=-59
-5π/2×2π+1=-5π^2+1=-49
π^2=10