
Пошаговое объяснение:
- Радиус r вписанной окружности в произвольный треугольник равен
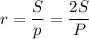
где S — площадь, p — полупериметр, P — соответственно, периметр.
- Радиус описанной окружности R связан с площадью так:
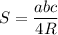
a, b и c — стороны треугольника.
Подставляем S из второго выражения в первое и домножаем на R:
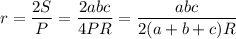
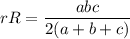
Для треугольника из условия две стороны равны 3, а вторая равна 2:
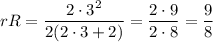
оль дает либо число кратное 10, либо произведение чисел 5 и 2 (числа оканчивающиеся на 5 и кратные 2).
Сколькими нулями оканчивается произведение натуральных чисел:
1) от 1 до 10
Кратные 10: 10 - 1 ноль
Оканчивающиеся на 5: 5 - 1 ноль
Итого 2 нуля.
2) от 15 до 24
Кратные 10: 20 - 1 ноль
Оканчивающиеся на 5: 15 - 1 ноль
Итого 2 нуля.
3) от 10 до 30
Кратные 10: 10, 20, 30 - 3 нуля
Оканчивающиеся 5: 15, 25 - здесь следует учесть, что 25=5*5 - 3 нуля
Итого 6 нулей
4) от 1 до 100
Кратные 10: 10, 20, 30, 40, 50 (5*10), 60, 70, 80, 90, 100 - 12 нулей
Оканчивающиеся 5: 5, 15, 25(5*5), 35, 45, 55, 65, 75(5*5*3),85,95 - 12
Итого 24 нуля
1) Чтобы найти радиус окружности, описанной вокруг произвольного треугольника, необходимо произведение его сторон разделить на четыре квадратных корня из полупериметра, умноженного на его разность с каждой стороной.
R=(2*3*3) :(4√(4*2*1*1)) =18:(4*2√2) =9/(4√2)
2) Пусть АС=2, ВН - высота к АС.
S = r * (a + b + c) : 2,
S=1/2* a* h. Высоту ищем из прямоугольного треугольника ВН=√(9-1) =2√2 => S=1/2*2*2√2=2√2 . Тогда
r=2√2*2:8=0,5√2.
3) R* r=9/(4√2) *0,5√2=9/8