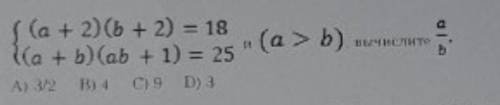
ответ: 4( вариант b)
Пошаговое объяснение: тут легко догадаться, что число 18 можно получить умножением 3 на 6. Т.е. в данном случае а = 4, б = 1, условие а больше б - соблюдено. (4+2)(1+2) = 18. Второе уравнение также верно: (4+1)(4*1+1) = 25. 4/1 = 4.


ответ: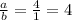
Объяснение:
чтобы чуть упростить вычисления, удобно сделать замену:
x = a+2; x > y (по условию)
y = b+2
получим систему:
можно решить второе уравнение относительно скобки (x+y)
t = x+y
(t-4)(23-2t) = 25
-2t² + 31t - 92 - 25 = 0
2t² - 31t + 117 = 0
корни: t = 13/2 и t = 9
y² - 9y + 18 = 0 по т.Виета корни:
y₁ = 3; x₁ = 9-3 = 6
y₂ = 6; x₂ = 9-6 = 3 (не подходит по условию x>y)
или
2y² - 13y + 36 = 0 D=169-288<0 нет корней
6 = a+2 --> a = 4
3 = b+2 --> b = 1