ответ: 17 кв. ед.
Пошаговое объяснение:
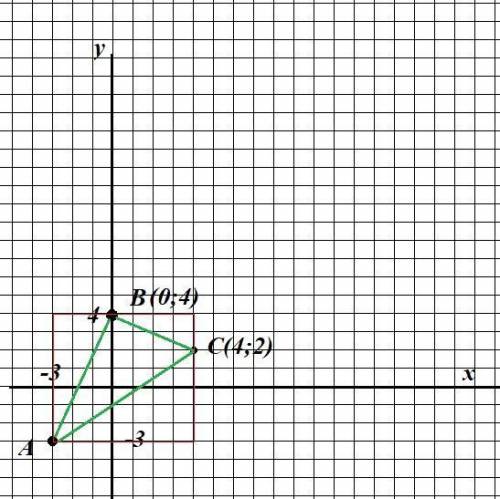
найдите площадь треугольника вершинами которого являются точки с координатами A(-3:-3); B(0;4); C(4;2).
-----------
Площадь треугольника по координатам его вершин определяем по формуле:
S=1/2*|(x1-x3)(y2-y3) - (x2-x3)(y1-y3)|;
Подставляем значения координат:
S=1/2*|(-3-4)(4-2) - (0-4)(-3-2)| = 1/2*|-14 - 20|=1/2*|-34|=17 кв. ед.
или по чертежу: (См. скриншот )
S=49-1/2*(3*7+2*4+7*5)=49-1/2*64= 17 кв. ед.
1.25см в квадрате
Пошаговое объяснение:
Проведем из точки М прямую МР параллельную основаниям трапеции и пересекающую диагональ ВД с точке Е.
Треугольники ВОС и МОЕ подобны по двум углам, тогда ОК / ОН = ОС / ОМ = 5 * Х /1 * Х.
Тогда длина отрезка КН = 6 * Х.
Продлим отрезок КН до пересечения с основанием АД.
Тогда КН / НЛ = ВМ / АМ = 2 / 1.
НЛ = КН / 2 = 3 * Х. Тогда КЛ = КН + НЛ = 9 * Х.
У треугольников ВОС и ВСД сторона ВС общая.
Тогда отношение их площадей равно отношению их высот.
Sвос / Sвсд = КЛ / КО = 5 * Х / 9 * Х = 5/9.
9 * Sвос = 5 * Sвсд.
Sвос = Sвсд – Sсод = Sвсд – 1. (умножим на 5)
5 * Sвос = 5 * Sвсд – 5.
5 * Sвос = 9 * Sвос – 5.
4 * Sвос = 5.
Sвос = 5/4 = 1,25 см2.
ответ: Площадь треугольника ВОС равна 1,25 см2.
17
Пошаговое объяснение: