Question

высота правильной треугольной пирамиды равна 4 корня из 2. чему равен объем этой пирамиды, если площадь ее боковой поверхности в три раза больше площади основания?​

Answer 1

$16\sqrt{6}$ куб. ед.

Пошаговое объяснение:

Пусть SABC -правильная треугольная пирамида.

$SO=4\sqrt{2}$ ед.

S(бок)=3S(осн)

Так как пирамида правильная, то треугольник АВС - правильный. Пусть сторона треугольника будет а.

Тогда площадь основания буден равна

$S=\dfrac{a^{2}\sqrt{3} }{4}$

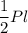S(бок)= $\dfrac{1}{2} Pl$,  где Р- периметр основания, а 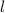$l$ - апофема.

$S=\dfrac{1}{2} \cdot3a\cdot l=\dfrac{3al}{2}$

Так как площадь боковой поверхности в 3 раза больше площади основания, то

$\dfrac{3al}{2} =\dfrac{3a^{2}\sqrt{3} }{4} |:3;\\\dfrac{al}{2} =\dfrac{a^{2}\sqrt{3} }{4} |\cdot4;\\2al=a^{2} \sqrt{3} |:a;\\2l=a\sqrt{3} ;\\l=\dfrac{a\sqrt{3} }{2}$

Рассмотрим треугольник SOM - прямоугольный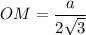 $OM= \dfrac{a}{2\sqrt{3} }$, как радиус окружности , вписанной в правильный треугольник АВС.

Применим теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

$SM^{2} =SO^{2} +OM^{2} \\SO^{2} =SM^{2}-OM^{2} ;\\(4\sqrt{2} )^{2} =\left(\dfrac{a\sqrt{3} }{2}\right )^{2} -\left(\dfrac{a}{2\sqrt{3} }\right )^{2} ;\\\\\dfrac{3a^{2} }{4} -\dfrac{a^{2} }{12} =16\cdot2;\\\\\dfrac{9a^{2}-a^{2} }{12} =32;\\\\\dfrac{8a^{2} }{12} =32;\\\\\dfrac{a^{2} }{12} =4;\\\\a^{2} =48$

Объем пирамиду определяется по формуле:

$V=\dfrac{1}{3} SH$

где $S-$ площадь основания, а Н - высота пирамиды.

$V=\dfrac{1}{3} \cdot \dfrac{a^{2} \sqrt{3} }{4} \cdot H;\\V= \dfrac{1}{3} \cdot \dfrac{48\sqrt{3} }{4} \cdot 4\sqrt{2}=\dfrac{48\sqrt{3} \cdot\sqrt{2} }{3}=16\sqrt{6}$

Значит, объем пирамиды равен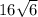 $16\sqrt{6}$ куб. ед.