Число делится на 9 если сумма цифр делится на 9
Число делится на 5 , если оканчивается на 0 или на 5.
Число делится на 45 , если оно делится на 5 и на 9 .
Таким образом у нас два варианта , последняя цифра 0 или 5 .
Сумма цифр должна делится на 9 , в середине 7 или 2
ответ : 570780 или 570285
31/56
Пошаговое объяснение:
1/8 и 3/7
1. Приведем к общему знаменателю. 8 и 7. Общий - 56 (их произведение)
2. Вписываем ниже черты ?/56 + ?/56
3. Делим новый знаменатель на старый и умножаем на числитель
1 Число - 56/8 = 7 и умножаем на числитель 1. 7*1 = 7 Значит первое число равно 7/56
2 Число - 56/7 = 8 и умножаем на числитель 3. 8*3 = 24. Значит второе число равно 24/56
4. Складываем полученные числа. 7/56 + 24/56
Получается 31/56.
Дробь не сокращается и не переводится в десятичную, следовательно ответ: 31/56
Дополнительные пояснения:
(Выше черты - числитель, ниже черты - знаменатель)
(В дробных числах складывают числители, при условии, что знаменатели равны)
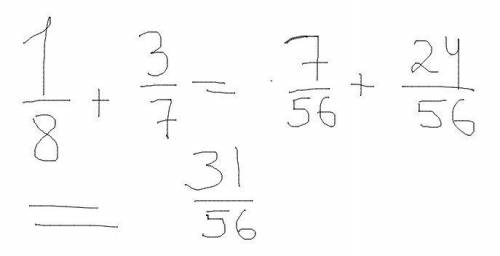
Прямая, проходящая через точку M1(x1; y1) и перпендикулярная прямой y=ax+b, представляется уравнением
y–y1=-1/a(x-x1) (1)
Альтернативная формула
Прямая, проходящая через точку M1(x1; y1) и перпендикулярная прямой Ax+By+C=0, представляется уравнением
A(y-y1)-B(x-x1)=0 (2)
Пошаговое объяснение:ПРИМЕР №1. Составить уравнение прямой, проходящей через точку (2; -1) и перпендикулярной 4x-9y=3.
Решение. Данную прямую можно представить уравнением y = 4/9x – 1/3 (a = 4/9). Уравнение искомой прямой есть y+1 = -9/4(x-2), т.е. 9x+4y-14=0.
ПРИМЕР №2. Решая пример 1 (A=4, B=-9) по формуле (2), найдем 4(y+1)+9(x-2)=0, т.е. 9x+4y-14=0.
ПРИМЕР №3. Составить уравнение прямой, проходящей через точку (-3, -2) перпендикулярно прямой 2y+1=0.
Решение. Здесь A=0, B=2. Формула (2) дает -2(x+3)=0, т.е. x+3=0. Формула (1) неприменима, так как a=0.
Два варианта: 570780 или 570285
Пошаговое объяснение:
Число кратно 45, значит кратно 9 и 5 (45=5*9)
Раз число делаится на 5, то оно оканчивается на 0 или на 5
1) оканчивается на 0
570*80
признак деления на 9 - сумма цифр делится на 9
5+7+0+8+0+цифра=20+цифра
для того, чтобы сумма цифр была кратна 9, нужно, чтобы цифра была равна 7 (единственный вариант)
2) оканчивается на 5
570*85
признак деления на 9 - сумма цифр делится на 9
5+7+0+8+5+цифра=25+цифра
для того, чтобы сумма цифр была кратна 9, нужно, чтобы цифра была равна 2 (единственный вариант в этом случае)