Пошаговое объяснение:
f'(t) = 3t^2 - 18t + 2 = 0
D4 = 81 - 6 = 75 = (5√3)^2
t1,2 = (9 ± 5√3)/3 = 3 ± 5/3 * √3
+ - +
3 - 5/3 * √33 + 5/3 * √3
/ \ /
Возрастает: x ∈ (-∞; 3 - 5/3 * √3] U [ 3 + 5/3 * √3; +∞)
Убывает: x ∈ [3 - 5/3 * √3; 3 + 5/3 * √3]
У Вас тут t с х смешалось, поэтому я подразумеваю, что t0 = 3
Уравнение касательной: f(t) = f'(t0) * (t - t0) + f(t0)
f'(t0) = 3*3^2 - 18*3 + 2 = -25
f(t0) = 3^3 - 9*3^2 + 2*3 +30 = -18
f(t) = -25 * (t - 3) - 18 = -25t + 57 - уравнение касательной
Графики приложены в вордовском файле
ответ: -1
Пошаговое объяснение:
Если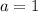
Система имеет решение
Если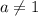
Графиком каждого уравнения системы является прямая
Система не имеет решений тогда и только тогда, когда данные две прямые не имеют общих точек
Для этого необходимо и достаточно, чтобы они были параллельны и не совпадали
Прямые параллельны в том случае, если у них равные угловые коэффициенты
Убедимся, что при найденных значениях параметра прямые не совпадают
При свободные коэффициенты равны
свободные коэффициенты равны 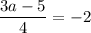 и
и 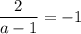 , значит при
, значит при  система не имеет решений
система не имеет решений
При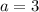 свободные коэффициенты равны
свободные коэффициенты равны 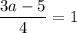 и
и 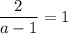 , значит при
, значит при 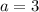 прямые совпадают и система имеет бесконечно много решений
прямые совпадают и система имеет бесконечно много решений