Question

42 певца записывают песню, в которой есть несколько куплетов и припевов в определенном порядке. Каждый куплет поется ровно
6 певцами, а каждый припев — ровно 4 певцами. Каждый певец
может спеть только в одном куплете или припеве, в песне есть хотя
бы один куплет и хотя бы один припев, два куплета не идут сразу друг
после друга, никакой припев не может быть одновременно до и после
припевов. Необязательно использовать всех певцов для записи. Сколько
различных количеств певцов нужно для исполнения таких песен?
Распишите поподробней решение .

Answer 1

Разберем структуру песни. Обозначим куплет как К, а припев как П.

Пусть в песне есть k куплетов:

$K_1\ K_2\ K_3\ \ldots\ K_k$

По условию, между куплетами может стоять 1 или 2 припева, а до первого и после последнего куплета - 0, 1 или 2 припева:

$\left(\begin{array}{c}\times\\\Pi\\\Pi\Pi\end{array}\right) K_1\left(\begin{array}{c}\Pi\\\Pi\Pi\end{array}\right) K_2\left(\begin{array}{c}\Pi\\\Pi\Pi\end{array}\right) K_3\left(\begin{array}{c}\Pi\\\Pi\Pi\end{array}\right) \ldots\ K_k\left(\begin{array}{c}\times\\\Pi\\\Pi\Pi\end{array}\right)$

Определим минимальное и максимальное возможное число припевов для k куплетов.

Минимальное число припевов соответствует случаю, когда между всеми куплетами стоит по одному припеву, а припевы до первого куплета и после последнего куплета отсутствуют. Так как промежутков между k куплетами (k-1), то этому же числу и равняется минимальное число припевов:

$\Pi_{\min}=k-1$

Заметим, что для одного куплета формула даст число припевов, равное нулю. Но по условию в песне есть хотя бы один припев. Тогда можно записать:

$\Pi_{\min}=\max(k-1;\ 1)$

Максимальное число припевов соответствует случаю, когда между всеми куплетами стоит по два припева, а также до первого куплета и после последнего куплета стоит по два припева. Тогда, максимальное число припевов:

$\Pi_{\max}=2(k-1)+2+2=2k-2+2+2=2k+2$

Рассмотрим песни с одним куплетом.

$k=1$

Тогда:

$\Pi_{\min}=1$

$\Pi_{\max}=2\cdot1+2=4$

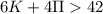Введем функцию $f(K;\ \Pi)=6K+4\Pi$, позволяющую по числу куплетов и припевов находить нужно число певцов. Можно ввести ограничение, например, о том, что при $6K+4\Pi42$ - функция не определена, так как по условию имеется 42 певца.

$f(1;\ 1)=6\cdot1+4\cdot1=\boxed{10}$

$f(1;\ 2)=6\cdot1+4\cdot2=\boxed{14}$

$f(1;\ 3)=6\cdot1+4\cdot3=\boxed{18}$

$f(1;\ 4)=6\cdot1+4\cdot4=\boxed{22}$

Рассмотрим песни с двумя куплетами.

$k=2$

Тогда:

$\Pi_{\min}=2-1=1$

$\Pi_{\max}=2\cdot2+2=6$

$f(2;\ 1)=6\cdot2+4\cdot1=\boxed{16}$

$f(2;\ 2)=6\cdot2+4\cdot2=\boxed{20}$

$f(2;\ 3)=6\cdot2+4\cdot3=\boxed{24}$

$f(2;\ 4)=6\cdot2+4\cdot4=\boxed{28}$

$f(2;\ 5)=6\cdot2+4\cdot5=\boxed{32}$

$f(2;\ 6)=6\cdot2+4\cdot6=\boxed{36}$

Рассмотрим песни с тремя куплетами.

$k=3$

Тогда:

$\Pi_{\min}=3-1=2$

$\Pi_{\max}=2\cdot3+2=8$

$f(3;\ 2)=6\cdot3+4\cdot2=\boxed{26}$

$f(3;\ 3)=6\cdot3+4\cdot3=\boxed{30}$

$f(3;\ 4)=6\cdot3+4\cdot4=\boxed{34}$

$f(3;\ 5)=6\cdot3+4\cdot5=\boxed{38}$

$f(3;\ 6)=6\cdot3+4\cdot6=\boxed{42}$

На этом шаге понятно, что последующие значения функции будут больше 42.

Рассмотрим песни с четырьмя куплетами.

$k=4$

Тогда:

$\Pi_{\min}=4-1=3$

$\Pi_{\max}=2\cdot4+2=10$

$f(4;\ 3)=6\cdot4+4\cdot3=36$

$f(4;\ 4)=6\cdot4+4\cdot4=\boxed{40}$

$f(4;\ 5)=6\cdot4+4\cdot542$

Последующие значения функции больше 42.

Рассмотрим песни с пятью куплетами.

$k=5$

Тогда:

$\Pi_{\min}=5-1=4$

$f(5;\ 4)=6\cdot5+4\cdot442$

Все значения функции в этом случае больше 42.

Таким образом, найденные различные количества певцов:

10, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42 - всего 16 значений

ответ: 16