А(4) и В(10), |4-10|=6
Пошаговое объяснение:
Определим координаты точек A и B:
1) Справа от точки 0 на единичной дальности отмечена число 1, что означает справа от точки 0 направление положительное и цена деления равна 1;
2) точка А отдалена от точки 0 на 4 единицы в положительном направлении, поэтому имеет координату 4, то есть А(4);
3) точка В отдалена от точки 0 на 10 единицы в положительном направлении, поэтому имеет координату 10, то есть В(10).
Расстояние между двумя точками А(x₁) и В(x₂) определяется по формуле AB= |x₁-x₂|. Поэтому расстояние между точками А(4) и В(10) равна |4-10|.
С другой стороны, по рисунку видно, что между точками А(4) и В(10) находится 6 единичных отрезков, поэтому расстояние между точками А(4) и В(10) равно 6.
Тогда |4-10|=6.
Сначала запишем формулы, которые понадобятся:
Площадь квадрата равна квадрату его стороны:
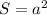
Отсюда, сторона квадрата равна корню квадратному из площади:

Периметр квадрата равен четырём его сторонам:

Подставим в эту формулу вместо стороны a корень из площади, и мы получим вот что:
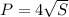
Так считается периметр для квадрата с площадью S
А если взять площадь в девять раз больше (то есть 9S ), то получим периметр P₂ , который равен:
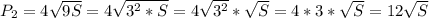
Во сколько раз увеличился периметр? Поделим новый периметр на старый, и узнаем (хоть это и так тут уже понятно).
Периметр увеличился в:
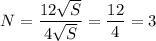 (раза)
(раза)
ответ: периметр увеличится в 3 раза
а) девять десятых, восемь целых четыре десятых, шесть целых двенадцать сотых, три сотых, двенадцать целых семь сотых.
б) пять целых пятьсот пятьдесят пять тысячных, девятьсот семьдесят шесть целых одна тысячная, восемьдесят четыре целых двадцать три тысячных, тысяча целых одна десятитысячная.