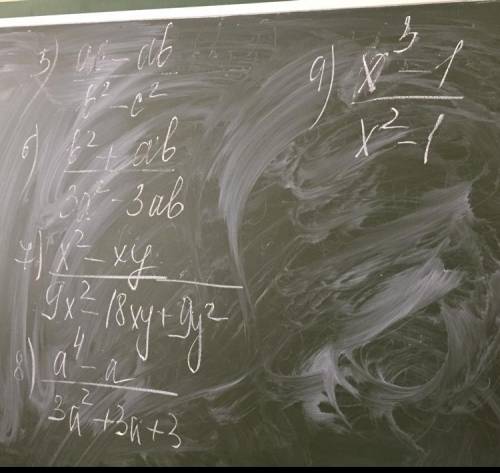
Объем прямоугольного параллелепипеда вычисляют по формулам:
V = abc, где a, b и c - его измерения (длина, ширина и высота);
V = Sосн · h, где Sосн - площадь основания (произведение длины и ширины), h - высота.
Площадь боковой поверхности прямоугольного параллелепипеда находят по формуле:
Sбок = Pосн · h, Росн = 2(а + b) - периметр основания, a и b - длина и ширина, h - высота.
Т.к. по условию а = 6 м, Sосн = 24 м², Sбок = 140 м², то:
1) 24 : 6 = 4 (м) - ширина b;
2) Росн = 2(6 + 4) = 20 (м) - периметр основания;
3) 140 : 20 = 7 (м) - высота h;
4) V = 6 · 4 · 7 = 168 (м³) - объем прямоугольного параллелепипеда.
ответ: 168 м³.
1:
а) 5/4<7/4
б) 1/6= 5/30 > 1/10=3/30
в)2 1/2= 5/2=2,54 < 3/5=23/5=4,8
г)1= 12/12 > 5/12
2:
а) 15/17 * 34/45=2/3
б)3 3/8*1 1/15= 27/8*16/15=3,6
в)11 2/3 : 3 4/5= 57/5 * 5/19=3
г)12:6/7=14
3:
(12 5/13 +у) - 9 6/13= 7 7\13
12 5/13 +у=17
у=17 - 12 5/13
у=4 8/13
4:
Приведем обе стороны к общему знаменателю 20
3 1/5=16/5=64/20
1/4=5/20
ширина: 64/20
длинна: 64/20-5/20=59/20
S=a*b=64/20*59/20= 236/25=9.44
5:
(7-2/3) : (1 3/4 - 1/6)*(1/2+ 2 2/3+1/6)= 6 1/3 :(7/4 - 1/6)*(3/6 + 16/6 + 1/6)=
=19/3:( 42/24-4/24)*(20/6)=19/3 : 38/24 * 20/6= 13 1/3
x² - y² = (x - y)(x + y)
x³ - y³ = (x - y)(x² + xy + y²)
(x - y)² = x² - 2xy + y²
(ac - ab)/(b² - c²) = a(c - b) / (b - c)(b +c) = - a/(b + c) (на c - b)
(b² + ab)/(3a² - 3ab) = b(a + b) / 3a(a - b) несократимая
(x² - xy)/(9x² - 18xy + 9y²) = x(x - y)/9(x - y)² = x/9(x - y) ( на x - y)
(a^4 - a)/(3a² + 3a + 3) = a(a³ - 1) / (3a² + 3a + 3) = a(a-1)(a² + a + 1)/3(a² + a + 1) = a(a - 1)/3 (на a² + a + 1)
(x³ - 1)/(x² - 1) = (x - 1)(x² + x + 1) /(x - 1)(x + 1) = (x² + x + 1)/(x + 1) (на x - 1)