Пусть х м в рулоне, тогда распишем по условию задачи расходы и остатки от пошива постельного белья:
Пододеяльник :
расход: 0,4 х - 6 (м)
остаток после пошива: х-0,4х+6 = 06 х +6 (м)
Простынь:
расход: 0,6(0,6х+6) - 4 = 0,36х+3,6-4=0,36х-0,4 (м)
остаток после пошива: 0,6х+6-0,36х+0,4=0,24х+6,4 (м)
Наволочка:
расход: (0,24х+6,4)*0,75-3=0,18х+4,8-3=0,18х+1,8 (м)
остаток после пошива:0,24х+6,4-0,18х-1,8=0,06х+4,6
Так как по условию задачи остаток составил 10 м, то составляем уравнение:
0,06х+4,6=10
0,06х = 5,4
х=5,4 : 0,06
х= 54 : 0,6
х=90 (м) в рулоне было
2) 0,36 * 90 -0,4= 32 (м) ушло на простыни
3) 0,4*90-6=36-6=30 (м) ушло на пододеяльники
4) 0,18*90+1,8=18 (м) ушло на наволочки
Проверка:
30+32+18= 80 (м) ушло на пошив
90-80 = 10 (м) остаток ткани
на фотографиях
Пошаговое объяснение:
10) нужно было привести q и сделать уравнение
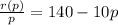
11) нужно представить рабочих в виде дроби (время)
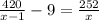 , так как первый рабочий затрачивает на 9 часов меньше, чем второй
, так как первый рабочий затрачивает на 9 часов меньше, чем второй
12) необходимо найти экстремумы функции в данном отрезке через первую производную. Так как функция представлена в виде перемножения 2 функций, то используем формулу y'=(u)'(v)'=u'v + v'u
Потом находим подходящее значение функции, которое должно находится между 5 и 14 по аргументу (x). После этого подставляем подходящее (10) в уравнение ФУНКЦИИ и находим значение y, которое равно 3. Получается что график функции будет выпуклым вниз на участке [5;14] в значении x = 10, а значении y = 3.




17:(2x-1,5):0,4=5 ^^^
34^*6"6+890-43=v---56158%