1. Пусть BM - высота h. Тогда треугольник ABM прямоугольный, причём AM = 0.5*AB, т.к. в равностороннем треугольнике высота делит сторону пополам, а стороны все равны. Пусть AB = BC = AC = x см, тогда AM = x/2
По теореме Пифагора
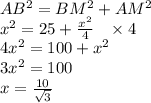
2. CK - высота. Т.к. треугольник равнобедренный, высота является также биссектрисой, то есть ∠ACK = 1/2·∠C = 45°. Тогда в треугольнике ACK ∠KAC = 90°-45° = 45°, то есть он равнобедренный и AK=CK = 6 см.
Тогда AB = 2AK = 5*2 = 10 см, т.к. CK делит AB пополам (св-во высоты равноб. тр-ка).
а) 7/3; члены отношения 7 и 3
б) 5/9; члены отношения 5 и 9
в) 12/4; члены отношения 12 и 4
г) 10/1000; члены отношения 10 и 1000