1)Не опаздывать на уроки. 2)Не брать в школу игрушки. 3)Беречь школьные учебники. 4)Сидеть за партой спокойно. 5)Не разговаривать на уроках. 6)Готовить одежду заранее. 7)Не скрывать от родителей плохие оценки. 8)Готовиться к уроку на перемене. 9)Не рисовать на партах,стульях. 10)Записывать домашнее задание в дневник. 11)Стараться писать в тетради красиво. 12)Не перебивать учителя. 13)Не бегать по школе. 14)Не выкрикивать с места. 14)Не сорить по школе. 15)Ходить в школьной форме. 16)Обращаться друг к другу по имени. 17)Не опаздывать на уроки. 18)Не материться. 20)Вовремя сдавать деньги.
Если имеются в виду двоичные числа, то всего будет 2^3 = 8 возможных комбинаций. Общая формула = a^n, где а - основание системы счисления, а n - соответственно количество цифр. Эту же формулу можно применить и для произвольной системы счисления, вместо a подставляя кол-во возможных значений каждой цифры. Естественно, что в таком случае кол-во вариантов должны быть одинаково для каждой цифры. Таким образом, снова получается 8 вариантов.
Если же подойти к вопросу более формально, считая что имеются в виду всем нам привычные десятичные числа, то в старших разрядах нулей быть не может. Т.о. получаем следующие варианты: 100, 101, 110, 111 - т.е. всего 4. Нетрудно заметить, что первая цифра всегда равна 1, т.о. кол-во вариантов от нее не зависит, оставшиеся две же вольны принимать любые значения. Получаем 2^2 = 4 - 4 варианта. Использована все та же формула, что и выше, меняются только параметры.
-15
Пошаговое объяснение:
Чтобы найти сумму целых решений неравенства, удовлетворяющих условию, составим систему неравенств и решим её.
решим первое неравенство
1 случай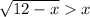 при х≥0
при х≥0
x∈(-4;3), но при х≥0 ⇒x∈[0;3)
2 случай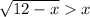 при х<0
при х<0
x∈R, но при при х<0 ⇒ x∈(-∞;0)
общее решение x∈(-∞;3)
решим второе неравенство
1 случай x<7 при х≥0 х∈[0;7)
2 случай -х<7, при х<0 х∈(-7;0)
общее решение x∈(-7;7)
найдем пересечение обоих решений и проверим ОДЗ x≤12
х∈(-7; 3)
Целые решения из полученного промежутка складываем и находим сумму: -6-5-4-3-2-1+0+1+2= -18