Математика: Я вас очень сильно 1 2 и 3

Я вас очень сильно 1 2 и 3

👇

Увидеть ответ

Ответ:

ДевочкаНадя

19.05.2021

Пошаговое объяснение:

1. 1) 5776, 346, 870, 378, 180, то есть все четные числа.

2) 25, 870, 1165, 180, 1575, то есть все числа оканчивающиеся на 5 или 0.

3) 870, 180, то есть все числа оканчивающиеся на ноль.

2. 386 < x < 401, при x = 388, 390, 392, 394, 396, 398, 400.

3. x - наибольшее двухзначное число.

(х+73):5 без остатка.

х будет равен 97.

4,5(49 оценок)

Открыть все ответы

Ответ:

Elvira2018

19.05.2021

Далее в тексте будем подразумевать под биквадратным трёхчленом и его коэффициентами выражение t^2 - 8 t + [7-a] = 0 ,

где под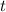

подразумевается квадрат переменной x^2 ,

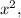т.е.

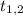а его корнями $t_{1,2}$ – квадраты искомых корней, если они различны, или его чётным корнем 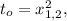$t_o = x^2_{1,2} ,$ если корень биквадратного трёхчлена t_o

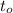– единственный.

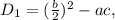Наше уравнение вообще имеет решения только тогда, когда дискриминант биквадратного трёхчлена неотрицателен, при этом, в силу чётности биквадратного уравнения, удобно находить чётный дискриминант через половину среднего коэффициента и без множителей в последнем слагаемом, т.е. по формуле $D_1 = ( \frac{b}{2} )^2 - ac ,$ тогда D_1 = 4^2 - [7-a] = 9 + a .

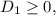Потребуем, чтобы $D_1 \geq 0 ,$ откуда следует, что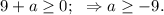 $9 + a \geq 0 ; \ \ \Rightarrow a \geq -9 .$

Уравнение не может стать просто квадратным, оно всегда будет иметь старшей степенью 4, поскольку старший коэффициент фиксирован и равен единице. Но биквадратное уравнение может выродится, когда его дискриминант равен нолю, что происходит при a = -9 ,

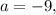а корень биквадратного трёхчлена станет чётным t_o = 4 ,

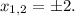давая два искомых корня $x_{1,2} = \pm 2 .$ Это значение a = -9

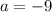как раз уже и есть одно из искомых решений для параметра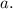 a .

Когда дискриминант больше нуля и биквадратное уравнение не вырождено, то квадратов искомых корней x^2 ,

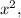всегда будет два – левый и правый (меньший и больший), однако при некоторых обстоятельствах левый квадрат искомых корней будет отрицательным, а значит, не будет давать пару искомых корней. Среднеарифметическое квадратов искомых корней x^2 ,

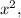по теореме Виета, в применении к биквадратному уравнению, будет равно числу, противоположному половине среднего коэффициента, т.е. оно равно 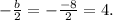$-\frac{b}{2} = -\frac{-8}{2} = 4 .$ Отсюда следует, что правый квадрат искомых корней x^2 ,

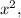– всегда положителен, а значит, всегда даёт два корня при положительном дискриминанте.

Левый же квадрат искомых корней отрицателен тогда и только тогда, когда этот левый квадрат лежит левее оси ординат, т.е. левее точки x = 0 .

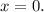А значит, значение всего трёхчлена x^4 - 8 x^2 + [7-a]

взятое от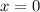

должно давать отрицательное значение, т.е. располагается в нижней межкорневой дуге параболы биквадратного трёхчлена.

Отсюда: $0^4 - 8 \cdot 0^2 + [7-a] < 0$ ;

7 - a < 0

;

;

О т в е т : $a \in \{ -9 \} \cup ( 7 ; +\infty ) .$

4,5(18 оценок)

Ответ:

nastyaemelika

19.05.2021

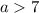1. Если Саша не дошёл до конца дистанции 0,2 её длины, значит, длина дистанции (120:0,8)=150 м. Во второй раз всю длину дистанции и ещё 0,1 её длины, то есть 1,1 дистанции. Выходит, он оценил дистанцию в (150*1,1)=165 шагов. ответ - Г. $\\$ 2. Скорость катера была 29632 м/ч; это равняется (29632:1000) км/ч, то есть 29,632 км/ч, что приблизительно равно 30 км/ч . ответ - Б. $\\$ 7.Если составить схему, видно, что с левого края стояли 9 женщин, а дальше мужчины и женщины чередовались. Выходит также, что последним стоял мужчина. Таким образом, мужчин было на 1 меньше, чем женщин.((50-9)+1):2=29 мужчин. ответ-В. $\\$ 8. Всего в олимпиадах участвовало (80-32)=48 человек. Из них в обеих олимпиадах участвовало ((37+33)-48)=22 ученика. ответ - Б. $\\$ 11.Может. $\\$ 12. 2016 год - високосный. Если 1 января этого года - пятница, то в нём 52 полные недели и 2 дня, из которых один - воскресенье. Значит, в 2016 г 53 воскресенья. Если убрать понедельники, то останется (366-52)=314 дней, в которых 52 полные недели и 2 дня, один из которых - воскресенье. В таком году тоже 53 воскресенья, хотя по-нашему их 45. Вероятность выпадения будет (53+45):7=14, то есть 14 раз в году. $\\$ 14.а. Нет, не могут. Б. Первым начал Петя. $\\$ простите, что не всё :( К сожалению, некоторые задачи решить не смогла.

4,4(83 оценок)

Это интересно:

Кулинария-и-гостеприимство

02.01.2021

Как устроить первоклассную вечеринку...

Дом-и-сад

04.01.2022

Солнечная энергия: идеальное решение для подогрева бассейна...

Компьютеры-и-электроника

30.11.2021

Apple Macintosh или другие ПК: как определиться с выбором...

Хобби-и-рукоделие