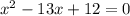
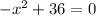
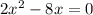
Нехай власна швидкість човна = х км/год. Тоді швідкість човна за течією річки = (х+2) км/год, а проти течії (х-2) км/год. Відстань, що проплив човен за течією річки, = (2,4 * (помнижити) ((х+2)) км,а відстань, яку проплив човен проти течії = (3,5 * (х-2)) км. Знаючи, що проти течії човен пройшов на 4,7 км мешне, ніж за течією, складемо і розв'яжемо рівняння:
3,5 * (х-2) - 2,4 (х+2) = 4,7
3,5х - 7 - 2,4х - 4,8=4,7
1,1х - 11,8 = 4,7
1,1х=16,5
х = 15
Отже, власна швидкість човна = 15 км/год.
Подробнее - на -
Дана точка А(-4; 3) и точки М(-1;2), Т(3;-1), через которые должна пройти прямая.
Надо найти расстояние от точки А до прямой МТ.
Для вычисления расстояния от точки M(Mx; My) до прямой Ax + By + C = 0 используем формулу:
d = |A·Mx + B·My + C|
√(A² + B²)
Для решения по этой формуле надо составить уравнение МТ в общем виде.
Вектор МТ = (3-(-1); -1-2) = (4; -3).
Составляем каноническое уравнение прямой МТ:
(x + 1(=)/4 = (y - 2)/(-3).
Преобразуем его в общее уравнение.
-3х - 3 = 4у - 8
Получаем: 3х + 4у - 5 = 0.
Здесь коэффициенты равны: А = 3, В = 4.
Подставим в формулу данные:
d = |3·(-4) + 4·3 + (-5)|
√(3² + 4²)
= |-12 + 12 - 5|
√(9 + 16)
= 5
√25 = 1
7х-3=6х+5
7х•6х=5-3
42х=2
х=2+42
х=44
остальное не знаю извини