Пошаговое объяснение:
21 - 1, 3, 7, 21
22 - 1, 2, 11, 22
30 - 1, 2, 5, 6, 10, 15, 30
48 - 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
54 - 1, 3, 6, 9, 18, 27, 54
1)Исходя из рисунка, выбросы Промышености, комунального хозяйства, транспорта и других источников равны 60 млн тонн, 40 млн тонн, 35 млн тонн и 20 млн тонн соответственно, то
Узнаем, на сколько млн тонн вклад уменьшится, если каждый источник сократили на 10%:
60*10=60*0.1=6(млн тонн)
40*10%=40*0.1=4(млн тонн)
35*10=35*0.1=3.5(млн тонн)
20*10=20*0.1=2(млн тонн)
Теперь узнаем, сколько млн тонн выбросов в 2010 году:
(60+40+35+20)-(6+4+3.5+2)=155-15.5=139.5(млн тонн)
Теперь пропорция:
155 млн тонн = 100%
139.5 млн тонн = х%
х=139.5*100/155=90%
100%-90%=10%
Значит, На 10% снизились бы в процентном отношении совокупные выбросы углекислого газа в 2010 году, если бы вклад каждого из источников сократился на 10%
2)Исходя из рисунка, в 1990 году выбросы углекислого газа составляло 30 млн тонн. То, значит
30*20%=30*0.2=6(млн тонн) - выбрасывают водный и воздушный транспорты.
2+1=3(части)
6/3=2(млн тонн) - одна часть
2*1=2(млн тонн) - составляют выбросы водного транспорта
Значит, если в 1990 году соотношение выбросов углекислоты воздушным и водным транспортом составляло 2:1, а их общая доля в выбросах транспорта - 20 %, то выбросы водного транспорта (в млн. т) равны 2 млн тонн
Пошаговое объяснение:
(см. объяснение)
Пошаговое объяснение:
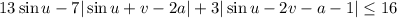
Введем замену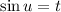 
. Откуда 
.
Тогда неравенство примет вид:
Пусть переменная здесь будет 
, а 
и 
параметры.
Наша задача определить, когда в решении этого неравенства будет содержаться промежуток ![[-1;\;1]](/tpl/images/2011/3499/001ed.png)
.
Заметим, что при любом раскрытии модулей перед буквой будет стоять положительное число.
Тогда при любых значениях параметров имеем возрастающую функцию 
.
Значит промежуток будет в решении неравенства, если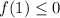 
, откуда переходим к новой записи:
Тогда пришли к неравенству:
Строим его в координатах 
и выделяем интересующую нас область:
(см. прикрепленный файл)
Итого при ![a\in\left[\dfrac{1}{5};\;\dfrac{3}{5}\right]](/tpl/images/2011/3499/9a62e.png)
исходное неравенство выполнимо для любой пары 
действительных чисел 
.
Задание выполнено!
1) 1, 2, 3, 7, 21 (простые: 2,3,7); 2) 1, 2, 3, 5, 6, 15, 30 (простые: 2,3,5);
3) 1, 2, 3, 4, 6, 8, 12, 16, 24, 48 (простые: 2,3);
4) 1, 2, 3, 6, 9, 18, 27, 54 (простые: 2,3