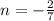 - знаменатель обращается в 0.
- знаменатель обращается в 0.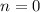 - по обычаю проверяется эта точка.
- по обычаю проверяется эта точка. (при
(при  →∞)
→∞)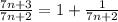

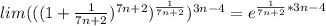 (при
(при  →∞)
→∞)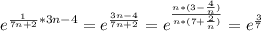 (при
(при  →∞)
→∞) →+∞ предел равен
→+∞ предел равен 
 →-∞ предел равен
→-∞ предел равен 
 →0 предел равен:
→0 предел равен:
 →
→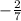
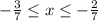 - мы получаем отрицательное основание).
- мы получаем отрицательное основание).
ответ: 22.1 y=sin(x)-x*cos(x); 22.2 y=4/9*sin(2*x)-1/3*x*cos(2*x)-5/9*sin(x).
Пошаговое объяснение:
22.1.
Функция y(x) имеет изображение y(p), функция y"(x) - изображение p²*y(p)-p*y(0)-y'(0), а функция f(x)=2*sin(x) - изображение 2/(p²+1). Так как по условию y(0)=y'(0)=0, то y"(x)⇒p²*y(p), и тогда уравнение принимает вид: p²*y(p)+y(p)=2/(p²+1). Отсюда y(p)=2/(p²+1)²=1/p*2*p/(p²+1). Так как функция y1(p)=1/p является изображением функции y1(x)=1, а функция y2(p)=2*p/(p²+1)² - изображением функции y2(x)=x*sin(x), то произведение y1(p)*y2(p) является изображением свёртки функций y1(x) * y2(x). Находим свёртку по формуле: y1(x) * y2(x)=F(x)-F(0), где F(t)=∫y1(t-τ)*y2(t)*dt. В нашем случае y1(t-τ)=1, y2(t)=t*sin(t), и тогда F(t)=∫t*sin(t)*dt=sin(t)-t*cos(t). Отсюда F(x)=sin(x)-x*cos(x), F(0)=0 и тогда y1(x) * y2(x)=sin(x)-x*cos(x). Тогда искомое решение y(x)=y1(x) * y2(x)=sin(x)-x*cos(x).
22.2
Функция y(x) имеет изображение y(p), функция y"(x) - изображение p²*y(p)-p*y(0)-y'(0), а функция f(x)=x*cos(2*x) - изображение (p²-4)/(p²+4)². Так как по условию y(0)=y'(0)=0, то y"(x)⇒p²*y(p), и тогда уравнение принимает вид: p²*y(p)+y(p)=(p²-4)/(p²+4)². Отсюда y(p)=(p²-4)/[(p²+4)²*(p²+1)]. Разлагая дробь справа на простейшие, находим y(p)=5/9*1/(p²+4)+8/3*1/(p²+4)²-5/9*1/(p²+1)=5/18*2/(p²+2²)+2/3*1/p*2*p*2/(p²+2²)²-5/9*1/(p²+1)=y1(p)+y2(p)-y3(p). Но функция y1(p)=5/18*2/(p²+2²) является изображением функции y1(x)=5/18*sin(2*x), а функция y3(p)=5/9*1/(p²+1) - изображением функции y3(x)=5/9*sin(x). Что же касается функции y2(p)=2/3*1/p*2*p*2/(p²+2²)², то она является изображением произведения числа 2/3 на свёртку функций y4(x) * y5(x). Так как изображением функции y4(x) является функция y4(p)=1/p, то y4(x)=1. Так как изображением функции y5(x) является функция y5(p)=2*p*2/(p²+2²)², то y5(x)=x*sin(2*x). Находим y4(x) * y5(x)=F(x)-F(0), где F(t)=∫y4(t-τ)*y5(t)*dt. Так как y4(t-τ)=1, а y5(t)=t*sin(2*t), то F(t)=∫t*sin(2*t)*dt=1/4*sin(2*t)-1/2*t*cos(2*t). Отсюда F(x)=1/4*sin(2*x)-1/2*x*cos(2*x) и F(0)=0, поэтому функция y2(p) является изображением функции y2(x)=2/3*[1/4*sin(2*x)-1/2*x*cos(2*x)]=1/6*sin(2*x)-1/3*x*cos(2*x). Отсюда искомое решение y(x)=5/18*sin(2*x)+1/6*sin(2*x)-1/3*x*cos(2*x)-5/9*sin(x)=4/9*sin(2*x)-1/3*x*cos(2*x)-5/9*sin(x).
сфоткай учебник если не знаешь то :
нажми на "+" потом на скребку