Математика: найти частное комплексных чисел: Z1 = -3 - 2i и Z2 = 4 + 3i

найти частное комплексных чисел: Z1 = -3 - 2i и Z2 = 4 + 3i

👇

Открыть все ответы

Ответ:

xDVadiKSlivE

18.09.2020

75344/10000 = 7,5344 (в десятичной) = 7 334/625 (в обыкновенной)
43/39 = 1 4/39
38/7=5 3/7
45/12=3,75 (в десятичной) = 3 3/4 (в обыкновенной)
231/100 = 2,31 (в десятичной) = 2 31/100 (в обыкновенной)
586/125=4,688 (в десятичной) = 4 86/125 (в обыкновенной)
8769/1000=8,769 (в десятичной) = 8 769/1000 (в обыкновенной)
39/6= 6 1/3
В преобразованной форме: 1 4/39; 2 31/100; 3 1/4; 4 86/125; 5 3/7; 6 1/3; 7 334/625; 8 769/1000
В исходной форме: 43/39; 231/100; 45/12; 586/125; 38/7; 38/6; 75344/10000; 8769/1000

4,5(99 оценок)

Ответ:

крут6776

18.09.2020

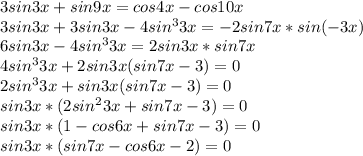
$3sin3x + sin9x = cos4x-cos10x\\3sin3x + 3sin3x - 4sin^33x = -2sin7x*sin(-3x)\\6sin3x - 4sin^33x = 2sin3x*sin7x\\4sin^33x + 2sin3x(sin7x-3) = 0\\2sin^33x + sin3x(sin7x-3) = 0\\sin3x*(2sin^23x + sin7x - 3) = 0\\sin3x*(1-cos6x + sin7x-3) = 0\\sin3x*(sin7x - cos6x - 2) = 0\\$

Проанализировав полученное уравнение, понимаем, что нулю оно равняется в двух случаях: когда первый множитель равен нулю или когда второй множитель равен нулю.

С первым все понятно: 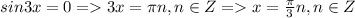$sin3x = 0 = 3x = \pi n, n \in Z = x = \frac{\pi}{3} n, n \in Z$

Теперь рассмотрим второй множитель: 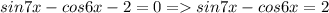sin7x - cos6x - 2 = 0 = sin7x - cos6x = 2

Так как функции sin и cos - это ограниченные функции, а именно не превышающие по модулю единицу, то такое равенство возможно тогда и только тогда, когда одновременно sin7x = 1, а cos6x = -1. Решим эти простые уравнения и найдем пересечение корней:

$sin7x = 1 = 7x = \frac{\pi}{2} + 2\pi k, k \in Z = x = \frac{\pi}{14} + \frac{2\pi}{7} k, k \in Z$

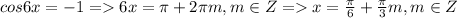
$cos6x = -1 = 6x = \pi + 2\pi m, m \in Z = x = \frac{\pi}{6} + \frac{\pi}{3}m, m \in Z$

Теперь приравняем полученные результаты:

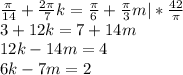
$\frac{\pi}{14} + \frac{2\pi}{7} k = \frac{\pi}{6} + \frac{\pi}{3}m |*\frac{42}{\pi}\\ 3 + 12k = 7 + 14m\\12k - 14m = 4\\6k - 7m = 2$

Заметим, что пара чисел k = 5 и m = 4 является решением, а значит, являются решением все числа вида:

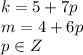
$k = 5 + 7p\\m = 4 + 6p\\ p \in Z$

Подставим это в любую серию корней и найдем пересечения (например, в первую):

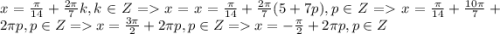
$x = \frac{\pi}{14} + \frac{2\pi}{7} k, k \in Z = x = x = \frac{\pi}{14} + \frac{2\pi}{7} (5+7p), p \in Z = x = \frac{\pi}{14} + \frac{10\pi}{7} + 2\pi p, p \in Z = x = \frac{3\pi}{2} + 2\pi p, p \in Z = x = -\frac{\pi}{2} + 2\pi p, p \in Z\\$