.(Красных шаров было на7 меньше, чем жёлтых, а зелёных шаров- на 10 больше, чем красных. на сколько меньше было жёлтых шаров, чем зелёных?).

👇

Увидеть ответ

Ответ:

mak57

09.02.2022

красные=желтые-7

зеленые=красн.+10=желтые-7+10

зеленые-красные=Ж-7+10-Ж=на 3

4,5(4 оценок)

Ответ:

мария2081

09.02.2022

10-7=3 шара

на три шара желтых меньше чем зеленых

4,6(91 оценок)

Открыть все ответы

Ответ:

ciromerka

09.02.2022

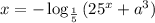
7. $x=-\log_{\frac{1}{5}}{(25^x+a^3)}$

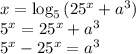
$x=\log_5{(25^x+a^3)}\\5^x=25^x+a^3\\5^x-25^x=a^3$

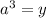Пусть a^3=y , количество корней от этого не изменится.

Рассмотрим функцию 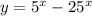y=5^x-25^x :

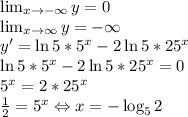
$\lim_{x \to -\infty}{y}=0\\ \lim_{x \to \infty}{y}=-\infty\\y'=\ln{5}*5^x-2\ln{5}*25^x\\\ln{5}*5^x-2\ln{5}*25^x=0\\5^x=2*25^x\\\frac{1}{2}=5^x\Leftrightarrow x=-\log_5{2}$

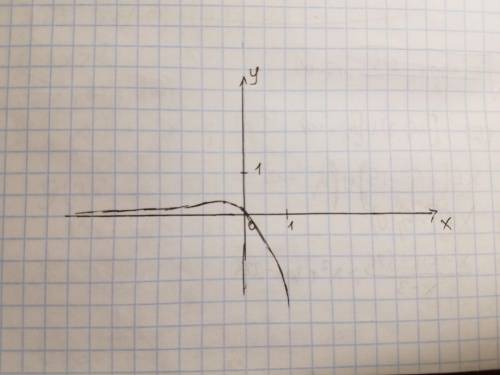
До точки экстремума функция возрастает, а после — убывает. Значит, это точка максимума. Максимальное значение функции равно 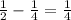$\frac{1}{2}-\frac{1}{4}=\frac{1}{4}$ . Прикинем график функции (см. рис. 1). Уравнение имеет 2 различных решения, если:

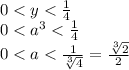
ответ: $(0; \frac{\sqrt[3]{2}}{2})$

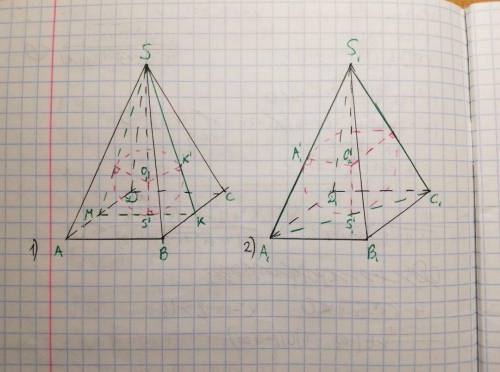
8. При изменении размеров пирамиды соотношения между соответственными элементами не изменятся, поэтому примем для простоты вычислений сторону основания за 1.

Рассмотрим первую пирамиду:

Пусть SKM — сечение пирамиды SABCD, где K и M — середины BC и AD соответственно. Тогда в это сечение попадает окружность, вписанная в треугольник SKM и касающаяся KM в точке S' (проекция точки S), SK в точке K'. Пусть ∠SKS' = α, KO₁ — биссектриса, тогда:

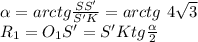
$\alpha=arctg \frac{SS'}{S'K}=arctg\ 4\sqrt{3}\\R_1=O_1S'=S'Ktg\frac{\alpha}{2}$

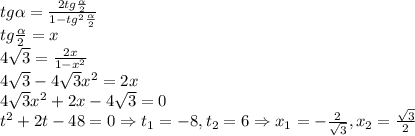
$tg\alpha=\frac{2tg\frac{\alpha}{2}}{1-tg^2\frac{\alpha}{2}}\\tg\frac{\alpha}{2} =x\\4\sqrt{3}=\frac{2x}{1-x^2}\\4\sqrt{3}-4\sqrt{3}x^2=2x\\4\sqrt{3}x^2+2x-4\sqrt{3}=0\\t^2+2t-48=0\Rightarrow t_1=-8, t_2=6 \Rightarrow x_1=-\frac{2}{\sqrt{3}}, x_2=\frac{\sqrt{3}}{2}$

Учитывая, что угол находится в первой четверти, 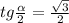$tg\frac{\alpha}{2}=\frac{\sqrt{3}}{2}$

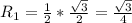
$R_1=\frac{1}{2}*\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{4}$

Рассмотрим вторую пирамиду:

Пусть S₁A₁C₁ — сечение пирамиды S₁A₁B₁C₁D₁. Это сечение содержит окружность, вписанную в треугольник S₁A₁C₁, касающуюся стороны A₁C₁ в точке S₁' (проекция точки S₁) и стороны S₁A₁ в точке A₁'. Пусть ∠S₁A₁S₁' = β, A₁O₂ — биссектриса. Тогда:

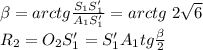
$\beta=arctg \frac{S_1S_1'}{A_1S_1'}=arctg\ 2\sqrt{6}\\R_2=O_2S_1'=S_1'A_1tg\frac{\beta}{2}$

Решая аналогичное уравнение, получаем 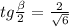$tg\frac{\beta}{2}=\frac{2}{\sqrt{6}}$

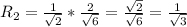
$R_2=\frac{1}{\sqrt{2}}*\frac{2}{\sqrt{6}}=\frac{\sqrt{2}}{\sqrt{6}}=\frac{1}{\sqrt{3}}$

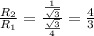
$\frac{R_2}{R_1}=\frac{\frac{1}{\sqrt{3}}}{\frac{\sqrt{3}}{4}}=\frac{4}{3}$

ответ: 4 : 3

4,4(46 оценок)

Ответ:

КеК5169

09.02.2022

Введите задачу...

Математический анализ Примеры

Популярные задачи

Математический анализ

Найти точки перегиба f(x)=2x^3-15x^2

f(x)=2x3−15x2f(x)=2x3-15x2

Найдем вторую производную.