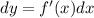 или
или 

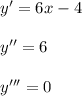


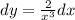
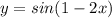




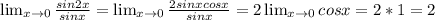
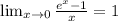
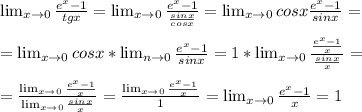
Из чисел 24; 576; 345; 970; 538; 4325; 8211; 1435; 960; 156230 запишите те которые делятся нацело на: 1)2 2)5 3)10
1) На двойку (2) делятся нацело числа кратные ей, то есть четные:
ответ: 24; 576; 970; 538; 960; 156230
2) На пятерку (5) делятся нацело числа, кратные ей, и оканчиваться они будут либо пятеркой (5) либо нулем (0), так как 5 + 5 = 10
ответ: 345; 970; 4325; 1435; 960 156230
3) На десятку (10) делятся нацело числа, кратные ей, причем оканчиваются они только нулем (0)
ответ: 970; 960; 156230
Пошаговое объяснение: