
Схема построение графика функции y=|x*(x-1)-5|=|x²-x-5|:
1. Сначала построим функцию у=х²-х-5:
а) Находим координаты вершины х0 и у0:
х0=-b/2a=1/2*1=1/2; y0=(1/2)²-1/2-5=-5 1/4.
б) Отмечаем вершину и проводим ось симметрии х=1/2.
в) Находим точки пересечения функции с осями координат OX и OY:
OX (y=0): x²-x-5=0;
D=1+20=21;
x1=(1-√21)/2≈-1,8; x2=(1+√21)/2≈2,8.
Точки пересечения с осью ОХ ((1-√21)/2; 0), ((1+√21)/2; 0).
OY (x=0): 0²-0-5=-5.
Точка пересечения с осью OY (0;-5).
г) Отмечаем на координатной плоскости точку симметричную точке (0;-5) относительно прямой х=1/2. Это точка (1;-5).
д) Соединяем полученные точки.
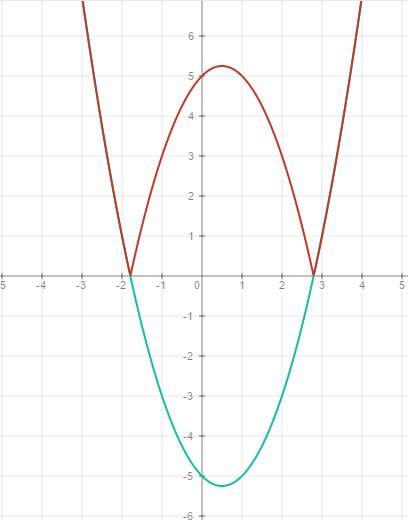
2. Теперь построим функцию у=|x²-x-5|:
ту часть функции, которая находится ниже оси ОХ нужно отразить вверх симметрично оси ОХ.
График готов.
метод интервалов:
х-π = 0; 2х +3 = 0; х - 4 = 0
х=π х = -1,5 х = 4
-∞ -1,5 π 4 +∞
- - + + это знаки (х - π )
- + + + это знаки (2х + 3)
- - - + это знаки (х - 4)
это решение неравенства
ответ: х ∈ (-∞; -1,5]∪[π; 4]