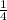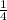. ответ представьте в виде десятичной дроби.
1).х км/ -скорость течения реки. 14+х -скорость по течению, а 14-х- скорость против течения. Составим уравнение 3*(14+х)=4*(14-х)
42+3х==56-4х
4х+3х=56-42. 7 х=14. х=2 - скорость течения реки
2). 1). 16*4=64 кв.м - площади прямоугольного и квадратного участков
2). корень из 64=8м - сторона квадратного участка
3). (16+4)*2=40м - надо на изгородь 1-го участка
4). 8*4=32м - надо на изгородь 2-го участка
5). 40-32= 8 м - длиннее изгородь 2-го участка
3). 6х-3-х+1=13. 5х-2=13. 5х=15. х=3
Как я понял условие, [(y/кор5)] - означает целую часть выражения в скобках.
Согласно методу Эйлера, решение дифф. ур-ия:
y' = f(x,y), где f(x,y) = x + cos[(y/кор5)] с нач. условием у0(1,8) = 2,6 на отрезке [1,8; 2,8] можно представить в виде:
у(k+1) = y(k) + h*f(xk, yk), где h = 0,1 - по условию.
Итак у(k=0) = 2,6
Теперь начинаем считать значения у, чтобы заполнить таблицу:
y1 = 2,6+0,1{1,9+cos[2,6/кор5])=2,6+0,1{1,9+cos1} = 2,8440
y2 = 2,8440+0,1{2,0+cos1} = 3,0980
y3 = 3,0980+0,1{2,1+cos1} = 3,3620
y4 = 3,3620 + 0,1{2,2+cos1} = 3,6360
y5 = 3,6360+0,1{2,3+cos1} = 3,9200
y6 = 3,9200+0,1{2,4+cos1) = 4,2140
y7 = 4,2140+0,1{2,5+cos1} = 4,5180
y8 = 4,5180+0,1{2,6+cos2) = 4,7364 (видим, что на этом шаге [y/кор5]=2)
y9 = 4,7364+0,1{2,7+cos2} = 4,9648
y10 = 4,9648+0,1{2,8+cos2} = 5,2032
x | y
|
1,8 | 2,6000
1,9 | 2,8440
2,0 | 3,0980
2,1 | 3,3620
2,2 | 3,6360
2,3 | 3,9200
2,4 | 4,2140
2,5 | 4,5180
2,6 | 4,7364
2,7 | 4,9648
2,8 | 5,2032
-0,5
Пошаговое объяснение:
(2x²+5x-3) : (х+3)
найдем корни квадратного трехчлена
2х²+5х-3=0
D=b²-4ac= 5²-4•2•(-3)=25+24=49>0, 2 корня
х₁=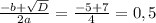
х₂=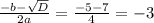
разложим квадратный трехчлен на множители, получаем
2(х-0,5) вычислим при х=