Пошаговое объяснение:
Взаимно простые числа — это числа, которые не имеют общих делителей кроме единицы.
Разложим числа 644 и 495 на простые множители. Простые множители — это те числа, которые имеют только два делителя, то есть делятся на единицу и сами на себя.
Тогда разложение числа 644 на простые множители будет равно:
644 = 2 * 2 * 23 * 7.
Разложение числа 495 на простые множители будет равно:
495 = 5 * 3 * 3 * 11.
Следовательно в данных в числах нет одинаковых делителей, то числа 644 и 495 являются взаимно простыми числами.
Дано :
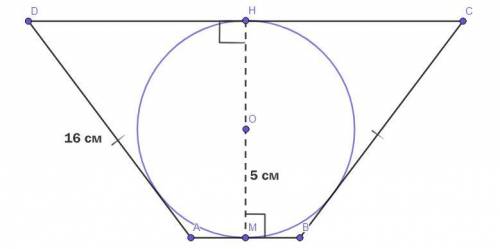
Четырёхугольник ABCD - равнобедренная трапеция (AB║DC, AD = BC).
Окружность с центром О - вписанная в равнобедренную трапецию окружность.
ОМ - радиус окружности = 5 см.
AD = BC = 16 см.
Найти :
S(ABCD) = ?
Если в четырёхугольник можно вписать окружность, то суммы противоположных сторон равны.
Следовательно -
AD + BC = AB + DC.
Но так как -
AD = BC = 16 см.
Поэтому -
AD + BC = 16 см + 16 см = 32 см
AB + DC = 32 см.
Радиус вписанной в трапецию окружности равен половине высоты.
На чертёже НМ - высота ABCD, следовательно -
НМ = 2*ОМ
НМ = 2*5 см
НМ = 10 см.
Площадь трапеции равна произведению полусуммы оснований и высоты.
То есть -
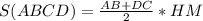
Теперь в формулу подставляем известные нам численные значения и считаем -
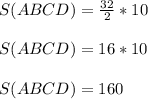
ответ : 160 (ед²).

Ці числа є взаємно простими
Пошаговое объяснение:
НСД(644;495)=
644/2
322/2
161/7
23/23
1
495/5
99/3
33/3
11/11
1